- ... arbitr\'aria1
-
Isto não está em contradição com as relações de incerteza. Elas dizem que não é
possível determinar simultaneamente posição e momento.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... qu\^antico2
- Abuso de linguagem. Todos os sistemas
são quânticos. A expressão correta seria ``sistema incorretamente descrito pela física
clássica''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... coordenadas3
- Ou melhor, o elemento de
volume em termos dessas coordenadas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... \'e.4
-
Na realidade, há quantidades físicas também da forma
onde 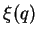 é outra função de onda. Como essas quantidades também devem permanecer
inalteradas, é necessário acrescentar que a trasformação
é outra função de onda. Como essas quantidades também devem permanecer
inalteradas, é necessário acrescentar que a trasformação
deve ser tal que o mesmo 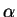 é usado para todas as funções de onda.
é usado para todas as funções de onda.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... completa.5
- Isto quer dizer que a função de onda de
cada uma das partes tem um ``futuro'' totalmente previsível, ou seja, que as duas partes do sistema
são independentes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...inuas.6
- Natura non facit saltus,
Isaac Newton.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....7
- Por exemplo, seja
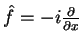 .
Então, dado
.
Então, dado 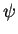 qualquer, temos
qualquer, temos
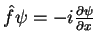 .
O operador
.
O operador 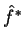 deve ser tal, então, que
deve ser tal, então, que
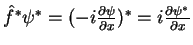 . Logo,
. Logo,
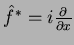 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... sistema.8
- Eqüivalentemente,
uma rotação
 sobre o sistema de eixos em
relação ao qual o sistema é referido.
sobre o sistema de eixos em
relação ao qual o sistema é referido.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Dirac9
- A
regra de Dirac diz: sejam
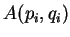 e
e 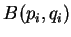 duas
quantidades físicas da mecânica clássica, e seja
duas
quantidades físicas da mecânica clássica, e seja 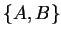 o
produto de Poisson (parênteses de Poisson) delas. Então, se
o
produto de Poisson (parênteses de Poisson) delas. Então, se
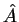 e
e 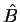 são os operadores hermitianos que
representam essas quantidades na mecânica quântica, temos a
igualdade simbólica:
são os operadores hermitianos que
representam essas quantidades na mecânica quântica, temos a
igualdade simbólica:
Ou seja, para obter o valor do comutador, calcula-se o produto de
Poisson das quantidades clássicas correspondentes,
multiplicando-se o resultado por 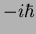 . Exemplo:
. Exemplo:
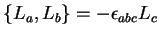 . Logo,
. Logo,
![$[\hat{L}_a,\hat{L}_b]=
i\hbar\epsilon_{abc} \hat{L}_c$](img376.png) .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...:10
-
Naturalmente eles não sabiam mecânica quântica, mas estudavam vibrações de corpos elásticos.Um dos
problemas dessa área, por exemplo, é a determinação das frequências que um tambor, de determinada forma,
pode emitir. Trata-se de um problema de autovalores: as freqüências emitidas são as autofreqüências.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... popular.11
- O leitor dedicado
gostará de investigar por que não aparece também um potencial
correspondente às forças de Coriolis.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... assintótico.12
- Ver, por exemplo, Dicke,
Wittke,Introduction to Quantum Mechanics, página 161.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Bohr!13
- Exercício: no modêlo pré-quântico de Bohr, das
órbitas de momento angular
 , determine o raio da menor
órbita estacionária. Você deverá encontrar
, determine o raio da menor
órbita estacionária. Você deverá encontrar 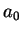 , o raio de Bohr.
, o raio de Bohr.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....14
- Estritamente,
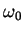 é a ``freqüência circular''. A verdadeira freqüência, que
é o inverso do período, é
é a ``freqüência circular''. A verdadeira freqüência, que
é o inverso do período, é
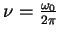 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
nome15
- A famosa transformada de Laplace!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... nota16
- Isto quer dizer que as energias
consideradas são positivas, como é o caso para um oscilador harmônico
de energia potencial
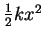
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...irculos17
- Bem, transforma círculos em elipses, mas, no
caso, a transformação é isotrópica, e transforma círculos em
círculos...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.