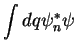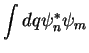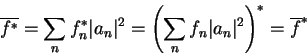Next: Adição e subtração de
Up: Operadores
Previous: Operadores
Vamos introduzir agora o conceito de valor médio 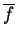 da quantidade
física
da quantidade
física 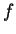 em um dado estado. Sejam
em um dado estado. Sejam  os valores possíveis de
os valores possíveis de 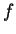 , ou seja, seus
autovalores. Sejam
, ou seja, seus
autovalores. Sejam  as probabilidades de cada um dos autovalores, no estado em
questão. Define-se então o valor médio como
as probabilidades de cada um dos autovalores, no estado em
questão. Define-se então o valor médio como
Usa-se também a notação
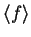 , para a mesma quantidade.
Queremos encontrar uma expressão para
, para a mesma quantidade.
Queremos encontrar uma expressão para 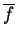 em termos da função de onda do
estado considerado. Seja
em termos da função de onda do
estado considerado. Seja 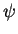 esta função. Para fazer isso vamos associar à quantidade
física
esta função. Para fazer isso vamos associar à quantidade
física 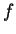 um operador linear
um operador linear 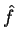 que atua sobre as funções de onda. Seja
que atua sobre as funções de onda. Seja  a função obtida quando
a função obtida quando 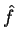 atua sobre
atua sobre 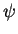 . Queremos, de
. Queremos, de 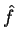 , que
, que
para qualquer estado 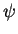 (lembre-se que estipulamos que as quantidades físicas deveriam
ser expressões bilineares na função de onda). Então,
(lembre-se que estipulamos que as quantidades físicas deveriam
ser expressões bilineares na função de onda). Então,
onde usamos
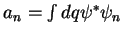 , obtido anteriormente. Vemos, primeiramente, que
, obtido anteriormente. Vemos, primeiramente, que
Ora,
de maneira que 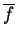 é linear, e que
é linear, e que
Sumarizando:
Os valores assumidos por uma quantidade física são reais. Portanto, os valores médios
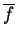 de uma quantidade física são também reais, como se vê de
de uma quantidade física são também reais, como se vê de
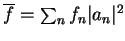 . Note-se (exercício fácil), que, se o estado
for uma autofunção de
. Note-se (exercício fácil), que, se o estado
for uma autofunção de 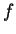 , o valor médio
, o valor médio 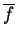 coincide com o autovalor de
coincide com o autovalor de 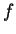 nesse estado.
Do fato de
nesse estado.
Do fato de 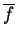 ser real segue uma propriedade importante dos operadores associados
a quantidades físicas:
ser real segue uma propriedade importante dos operadores associados
a quantidades físicas:
 |
(5) |
Ora,
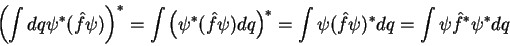 |
(6) |
onde 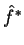 é definido assim: se
é definido assim: se
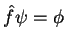 , então
, então 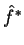 é o operador
tal que
é o operador
tal que
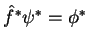 .7
Então,
.7
Então,
Vamos definir o operador transposto 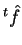 do operador
do operador 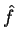 . Sejam
. Sejam 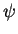 e
e 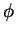 funções arbitárias. Então
funções arbitárias. Então 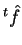 é tal que
é tal que
Por exemplo,
Da condição de realidade de 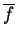 , Eq.(6), temos
, Eq.(6), temos
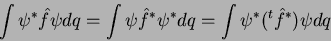 |
(7) |
Comparando os dois extremos vemos que
Operadores com esta propriedade são ditos hermiteanos. Logo, os operadores associados a
quantidades físicas são operadores lineares hermiteanos.
Podemos, formalmente, considerar quantidades físicas complexas, isto é, cujos autovalores são
complexos. Por exemplo, dadas as coordenadas 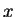 e
e 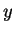 ,podemos considerar a quantidade
,podemos considerar a quantidade 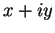 . Seja
. Seja
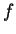 uma quantidade desse tipo, e seja
uma quantidade desse tipo, e seja 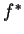 a quantidade cujos autovalores são os complexo-conjugados
dos autovalores de
a quantidade cujos autovalores são os complexo-conjugados
dos autovalores de 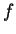 . À quantidade
. À quantidade 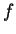 corresponde o operador
corresponde o operador 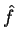 . Denotemos por
. Denotemos por  o operador correspondente à quantidade
o operador correspondente à quantidade 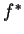 . Este operador é denominado o adjunto
de
. Este operador é denominado o adjunto
de 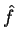 .
O valor médio da quantidade
.
O valor médio da quantidade 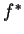 é dado por
é dado por
onde apenas adaptamos a definição de média de um operador.
Ora,
logo,
Mas
Ou seja,
Comparando, temos
Em palavras, o adjunto é o transposto do conjugado.
A condição de hermiticidade de um operador, escrita anteriormente como
pode agora ser escrita:
e os operadores hermiteanos são aqueles que coincidem com os adjuntos. Daí serem
chamados também de auto-adjuntos.
Vamos agora mostrar que a ortogonalidade das autofunções de um operador hermiteano pode ser demonstrada diretamente.
Sejam  e
e 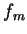 dois autovalores diferentes do operador hermiteano
dois autovalores diferentes do operador hermiteano 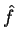 .
Sejam
.
Sejam  e
e  as autofunções correspondentes. Então,
as autofunções correspondentes. Então,
Multiplicando a primeira por  , temos
, temos
e
 |
(10) |
Tomando o complexo conjugado de (9) e multiplicando por  ,
temos
,
temos
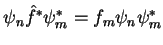 . Integrando,
. Integrando,
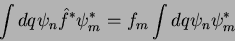 |
(11) |
 |
(12) |
Mas
pois 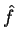 é hermiteano. Logo, o primeiro termo de (12) é zero.
Conseqentemente,
é hermiteano. Logo, o primeiro termo de (12) é zero.
Conseqentemente,
e, como 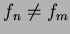 , segue que
, segue que



Next: Adição e subtração de
Up: Operadores
Previous: Operadores
Henrique Fleming
2003-03-30