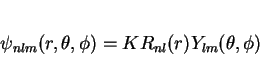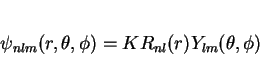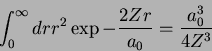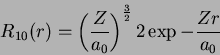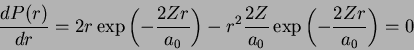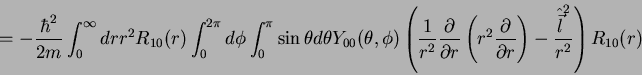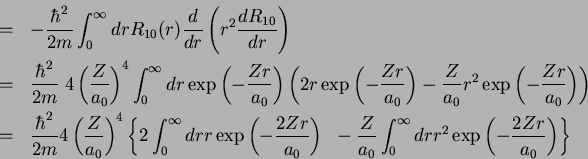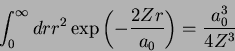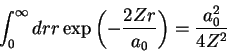Next: As desigualdades de Heisenberg
Up: O átomo de Hidrogênio
Previous: As soluções da equação
Até agora escrevemos as funções de onda assim:
Como determinar a constante 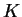 ? Uma vez que os harmônicos
esféricos são normalizados por conta própria, pois
? Uma vez que os harmônicos
esféricos são normalizados por conta própria, pois
devemos ter
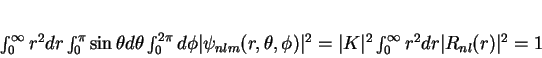 |
(176) |
Exemplo: para o estado 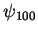 ,
,
Usando
obtemos
confirmando o valor da tabela.
De posse da expressão detalhada da função de onda, podemos fazer
perguntas interessantes. Qual é a probabilidade de o elétron
estar, no estado fundamental do átomo de hidrogênio, entre 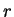 e
e
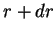 ? Ela é dada por
? Ela é dada por
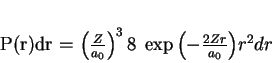 |
(177) |
Para que valor de 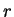 a probabilidade é máxima (para idêntidos
a probabilidade é máxima (para idêntidos
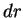 )? No ponto de máximo, teremos
)? No ponto de máximo, teremos
ou
Logo, para o átomo de hidrogênio (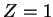 ), temos que a
probabilidade máxima é para
), temos que a
probabilidade máxima é para 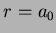 , o raio de
Bohr!13
Vamos calcular agora a velocidade média do elétron no estado
fundamental.
, o raio de
Bohr!13
Vamos calcular agora a velocidade média do elétron no estado
fundamental.
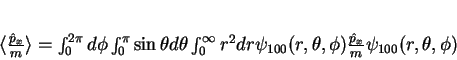 |
(178) |
Usando
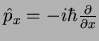 e
e
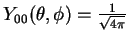 , obtemos
, obtemos
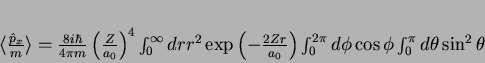 |
(179) |
onde usamos
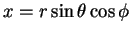 . Como
. Como
temos que o valor médio da componente 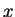 da velocidade do elétron
no estado fundamental é 0. Como o estado é esfericamente
simétrico, o mesmo resultado deve valer para as outras
componentes. Logo,
da velocidade do elétron
no estado fundamental é 0. Como o estado é esfericamente
simétrico, o mesmo resultado deve valer para as outras
componentes. Logo,
Isto posto, podemos dizer que e elétron está em repouso, no estado
fundamental? Certamente não! Em qualquer modêlo clássico com
órbita circular (qualquer órbita fechada, de fato) o elétron está
em movimento e sua velocidade média é zero. Para obter mais
informações sobre o que o elétron faz no estado fundamental do
átomo de hidrogênio, vamos calcular sua energia
cinética média. Ela é dada por:
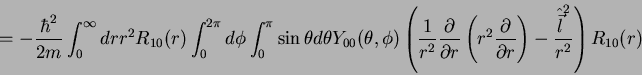 |
(180) |
Usando as integrais
e
obtemos o resultado, para 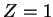 ,
,
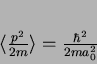 |
(181) |
Logo, o elétron não está parado. E nem poderia: se tivesse momento
perfeitamente definido (no caso, nulo), sua posição teria de ser
totalmente indefinida, pelo princípio da incerteza. Como a
incerteza na posição é da ordem de 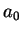 e, da
Eq.(182), vemos que a incerteza no momento é da ordem
de
e, da
Eq.(182), vemos que a incerteza no momento é da ordem
de
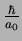 , vemos que o produto das incerteza é da
ordem de
, vemos que o produto das incerteza é da
ordem de 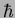 . Ou seja, o elétron tem o mínimo movimento
exigido pelo princípio de incerteza. Está tão parado quanto é
possível!
. Ou seja, o elétron tem o mínimo movimento
exigido pelo princípio de incerteza. Está tão parado quanto é
possível!



Next: As desigualdades de Heisenberg
Up: O átomo de Hidrogênio
Previous: As soluções da equação
Henrique Fleming
2003-03-30