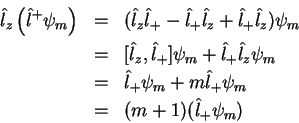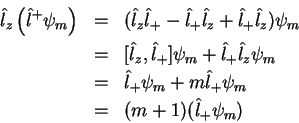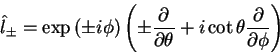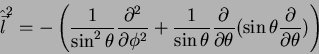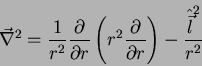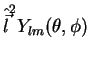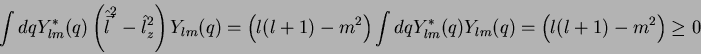Next: Construção dos harmônicos esféricos
Up: Autofunções do momento angular
Previous: As autofunções da componente
Seja 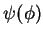 a autofunção de
a autofunção de 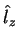 de
autovalor
de
autovalor 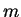 . Calculemos
. Calculemos
Logo, se
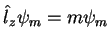 , então
, então
Analogamente se mostra que
Assim, usando os operadores 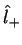 e
e 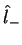 , pode-se
varrer todo o espectro do operador
, pode-se
varrer todo o espectro do operador 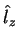 .
Considere o operador
.
Considere o operador
Lema:Se 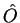 é hermiteano,
é hermiteano,
para qualquer estado.
Demonstração:
Em particular, segue que
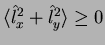 , logo,
, logo,
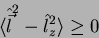 |
(93) |
A construção das autofunções de
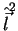 é facilitada pelo fato
de que a expressão de
é facilitada pelo fato
de que a expressão de
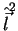 é um operador diferencial familiar à
física clássica. De fato, um cálculo direto leva a
é um operador diferencial familiar à
física clássica. De fato, um cálculo direto leva a
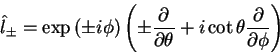 |
(94) |
e, como
obtém-se
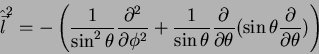 |
(95) |
Acontece que o laplaceano em coordenadas esféricas é
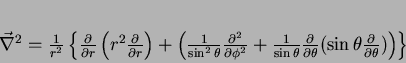 |
(96) |
ou seja,
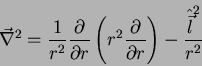 |
(97) |
Os físicos do século XIX resolveram o problema de determinar as autofunções de
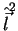 :10
essas funções são os harmônicos esféricos,
:10
essas funções são os harmônicos esféricos,
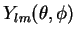 , que satisfazem as equações
de autovalores
, que satisfazem as equações
de autovalores
Os harmônicos esféricos são muito bem conhecidos. Para um estudo deles no contexto clássico
as minhas referências preferidas são Courant [4] e Sommerfeld [7]. Nessas notas,
usando técnicas que introduziremos a seguir, construiremos explicitamente os 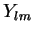 . Para o momento
é suficiente informar que
. Para o momento
é suficiente informar que
ou seja, é o produto de uma função de 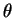 por uma autofunção de
por uma autofunção de 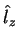 .
Uma observação importante: as autofunções de
.
Uma observação importante: as autofunções de 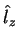 são as funções
são as funções
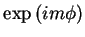 para
qualquer inteiro
para
qualquer inteiro 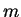 . Quando construirmos as autofunções comuns a
. Quando construirmos as autofunções comuns a
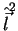 e
e 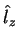 , veremos que
, veremos que 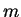 sofrerá mais restrições. De fato, como temos
sofrerá mais restrições. De fato, como temos
segue que
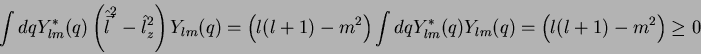 |
(100) |
Portanto, dado 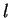 ,
, 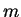 não pode ser qualquer inteiro. O maior valor permitido
é tal que
não pode ser qualquer inteiro. O maior valor permitido
é tal que
Vê-se imediatamente que 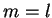 é permitido, mas
é permitido, mas 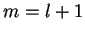 é proibido. Logo,
o máximo valor permitido de
é proibido. Logo,
o máximo valor permitido de 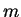 para as autofunções
para as autofunções 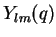 é
é
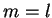 . Um argumento an'alogo mostra que o menor é
. Um argumento an'alogo mostra que o menor é 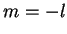 . Resumindo,
. Resumindo,
Neste intervalo,
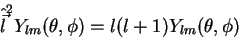 |
(101) |
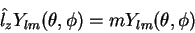 |
(102) |
Assim, para cada 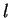 há
há  valores distintos de
valores distintos de 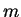 .
.
Subsections



Next: Construção dos harmônicos esféricos
Up: Autofunções do momento angular
Previous: As autofunções da componente
Henrique Fleming
2003-03-30