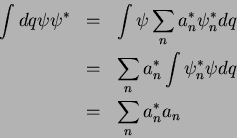Next: Valor médio
Up: Mecânica Quântica
Previous: O princípio da incerteza
Seja 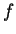 uma quantidade física que caracteriza o estado de um sistema quântico.
Os valores que uma dada quantidade física pode assumir são chamados de
autovalores. O conjunto dos autovalores é o espectro. Na mecânica
clássica as quantidades físicas são contínuas.6 Na mecânica quântica, não necessariamente. Pode haver espectros discretos
ou espectros contínuos. Vamos supor, para simplificar, que o espectro de
uma quantidade física que caracteriza o estado de um sistema quântico.
Os valores que uma dada quantidade física pode assumir são chamados de
autovalores. O conjunto dos autovalores é o espectro. Na mecânica
clássica as quantidades físicas são contínuas.6 Na mecânica quântica, não necessariamente. Pode haver espectros discretos
ou espectros contínuos. Vamos supor, para simplificar, que o espectro de 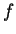 seja discreto.
Os autovalores de
seja discreto.
Os autovalores de 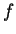 serão denotados por
serão denotados por 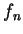 ,
, 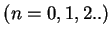 . A função de onda do sistema,
no estado em que
. A função de onda do sistema,
no estado em que 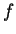 tem o valor
tem o valor 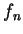 , será denotada por
, será denotada por 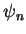 . Essas funções são chamadas
autofunções de
. Essas funções são chamadas
autofunções de 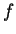 . Para cada uma delas,
. Para cada uma delas,
Um dos princípios básicos da mecânica quântica é este:
(I) O conjunto das autofunções de uma quantidade física 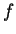 é completo. Isto é, dada uma função de onda
qualquer
é completo. Isto é, dada uma função de onda
qualquer 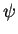 do sistema, podemos expandí-la em autofunções de
do sistema, podemos expandí-la em autofunções de 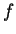 assim:
assim:
onde os  são números complexos.
são números complexos.
(II)Fazendo-se uma medida de 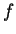 em
em 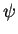 , a probabilidade de se obter o valor
, a probabilidade de se obter o valor 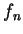 é dada
por
é dada
por  .
.
Em conseqüência, devemos ter
pois
 é a probabilidade de, medindo-se
é a probabilidade de, medindo-se 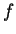 , obter-se qualquer um dos valores
possíveis.
Temos, então, o resultado
, obter-se qualquer um dos valores
possíveis.
Temos, então, o resultado
Por outro lado, temos
logo,
de onde se conclui que
Finalmente, usando
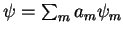 , temos
, temos
de onde se conclui que
Diz-se então que as autofunções são ortogonais.
Subsections



Next: Valor médio
Up: Mecânica Quântica
Previous: O princípio da incerteza
Henrique Fleming
2003-03-30