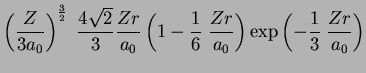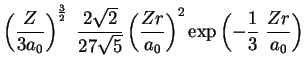Next: Algumas propriedades do átomo
Up: O átomo de Hidrogênio
Previous: Determinando o comportamento assintótico
Vamos então procurar soluções da Eq.(140) da forma
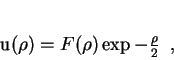 |
(149) |
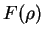 sendo um polinômio em
sendo um polinômio em 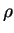 . A razão de ser um
polinômio é que o comportamento assintótico de (149)
deve ainda ser dado pelo termo exponencial, o que é garantido se
. A razão de ser um
polinômio é que o comportamento assintótico de (149)
deve ainda ser dado pelo termo exponencial, o que é garantido se
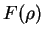 for um polinômio. Uma análise mais fina mostraria que,
se se admitisse que
for um polinômio. Uma análise mais fina mostraria que,
se se admitisse que 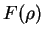 fosse uma série infinita, sua soma
seria essencialmente uma exponencial em
fosse uma série infinita, sua soma
seria essencialmente uma exponencial em 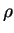 , alterando o
comportamento assintótico.12
Seja
, alterando o
comportamento assintótico.12
Seja 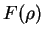 uma expressão da forma
uma expressão da forma
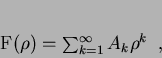 |
(150) |
onde a potência mais baixa é a primeira para assegurar que
Derivando termo a termo, temos
Inserindo estas expressões na Eq.(150), temos
![\begin{displaymath}
\sum_{k=1}^{\infty}\left\{k(k-1)A_{k}\rho ^{k-2}-kA_{k}\rh...
...}{\rho}-\frac{l(l+1)}{\rho
^2}\right]A_{k}\rho^{k}\right\}=0
\end{displaymath}](img542.png) |
(151) |
O coeficiente da potência  de
de 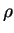 é dado por
é dado por
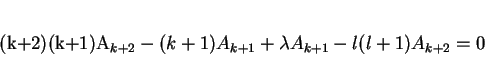 |
(152) |
para que a equação diferencial seja satisfeita termo a termo.
Diminuindo o valorde  de uma unidade, temos uma relação mais
conveniente:
de uma unidade, temos uma relação mais
conveniente:
![\begin{displaymath}
A_{k+1}\left[(k+1)k-l(l+1)\right] = (k-\lambda) A_k
\end{displaymath}](img544.png) |
(153) |
ou, equivalentemente,
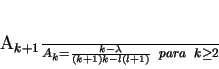 |
(154) |
Para os índices mais baixos temos as equações
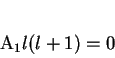 |
(155) |
![\begin{displaymath}
\left[2-l(l+1)\right]A_2 + (\lambda -1)A_1 =0
\end{displaymath}](img547.png) |
(156) |
A equação (154) é muito importante. Dela vemos que, para
que a série se interrompa em algum ponto, tornando-se um
polinômio, devemos ter que  . Ora, os
. Ora, os  são
inteiros, logo, a condição para que a série se interrompa é que
exista um inteiro
são
inteiros, logo, a condição para que a série se interrompa é que
exista um inteiro 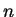 tal que
tal que
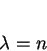 |
(157) |
Como
temos
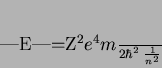 |
(158) |
ou, eqüivalentemente,
 |
(159) |
que é a fórmula de Bohr! Voltando ao cálculo das autofunções, além
da condição 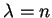 , devemos ter que
, devemos ter que
 , de
outra forma, na equação (154), o denominador se anularia
ao mesmo tempo que o numerador, não garantindo o anulamento do
coeficiente
, de
outra forma, na equação (154), o denominador se anularia
ao mesmo tempo que o numerador, não garantindo o anulamento do
coeficiente 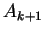 . Portanto devemos ter
. Portanto devemos ter 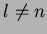 .
Vamos construir as primeiras soluções. Tomemos
.
Vamos construir as primeiras soluções. Tomemos
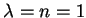 A
este valor corresponde a energia
A
este valor corresponde a energia
que é a energia do estado fundamental do átomo de
hidrogênio (o de energia mais baixa). Para este valor de 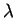 podemos ter
podemos ter 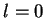 , mas não
, mas não 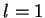 . Então, das equações
. Então, das equações
temos Que 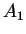 é indeterminado, e
é indeterminado, e  , assim como os
coeficientes de índice mais alto. Temos então, para a solução,
, assim como os
coeficientes de índice mais alto. Temos então, para a solução,
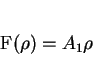 |
(160) |
e
 |
(161) |
Em termos de 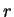 , usando
, usando
e introduzindo
denominado raio de Bohr, obtemos, após cálculos simples,
Para o estado fundamental, temos, então,
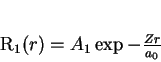 |
(162) |
que é também a função completa, pois 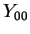 é constante.
Para
é constante.
Para
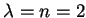 temos as possibilidades
temos as possibilidades 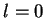 e
e 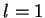 . Para
o primeiro caso, temos, novamente,
. Para
o primeiro caso, temos, novamente, 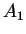 indeterminado. Para
indeterminado. Para
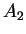 , usamos a equação (153), que dá
, usamos a equação (153), que dá
ou seja,
A solução então é
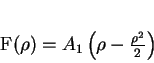 |
(163) |
e
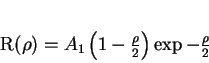 |
(164) |
Expressando em termos de 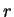 , obtemos
, obtemos
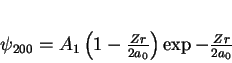 |
(165) |
onde usamos a notação tradicional para os autoestados do átomo de
hidrogênio:
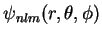 . O leitor, neste ponto,
deveria ser capaz de mostrar que
. O leitor, neste ponto,
deveria ser capaz de mostrar que
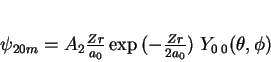 |
(166) |
No segundo caso, 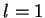 ,vemos, da Eq.(155), que
,vemos, da Eq.(155), que
enquanto 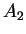 é indeterminado.
é indeterminado. 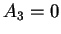 , assim como os índices
mais altos. Logo,
, assim como os índices
mais altos. Logo,
A expressão em termos de 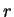 vem a ser
vem a ser
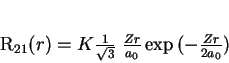 |
(167) |
Como vimos, a função radial fica definida quando se dão os valores
de 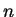 e
e 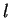 . Por isso ela é denotada por
. Por isso ela é denotada por 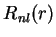 . Para o caso
de
. Para o caso
de 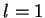 a dependência angular não é trivial.pois temos
a dependência angular não é trivial.pois temos
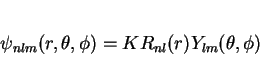 |
(168) |
que, nesse caso dá
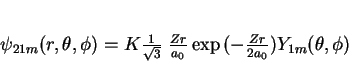 |
(169) |
com 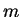 podendo tomar os valores 1, 0, e -1.
Note que a energia fica totalmente determinada por
podendo tomar os valores 1, 0, e -1.
Note que a energia fica totalmente determinada por 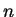 . Então,
exceto pelo estado fundamental, a cada nível de energia
correspondem mais de um estado do sistema. O espectro é dito
degenerado (no bom sentido!). Considere, por exemplo,
o nível de energia com
. Então,
exceto pelo estado fundamental, a cada nível de energia
correspondem mais de um estado do sistema. O espectro é dito
degenerado (no bom sentido!). Considere, por exemplo,
o nível de energia com 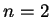 . Podemos ter
. Podemos ter 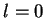 , que dá um único
estado, ou
, que dá um único
estado, ou 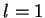 , que admite 3 valores de
, que admite 3 valores de 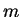 . No total, então, há
4 estados neste nível de energia. Diz-se que o grau de
degenerescência é 4. É fácil provar que o grau de degenerescência
do nível
. No total, então, há
4 estados neste nível de energia. Diz-se que o grau de
degenerescência é 4. É fácil provar que o grau de degenerescência
do nível 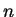 é
é 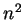 . O numero quântico
. O numero quântico 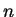 é denominado
número quântico principal.
A seguir apresentamos uma lista das partes radiais de algumas
funções de onda do átomo de hidrogênio.
é denominado
número quântico principal.
A seguir apresentamos uma lista das partes radiais de algumas
funções de onda do átomo de hidrogênio.
 |
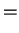 |
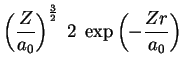 |
(170) |
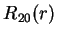 |
 |
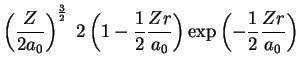 |
(171) |
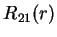 |
 |
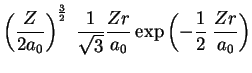 |
(172) |
 |
 |
![$\displaystyle \left(\frac{Z}{3a_0}\right)^{\frac{3}{2}}\;2\left[1-\frac{2}{3}\f...
...(\frac{Zr}{a_0}\right)^2\right]
\exp{\left(-\frac{1}{3}\;\frac{Zr}{a_0}\right)}$](img595.png) |
(173) |
 |
 |
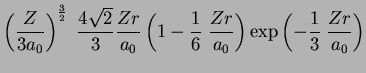 |
(174) |
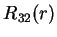 |
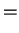 |
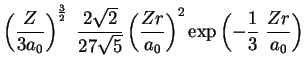 |
(175) |



Next: Algumas propriedades do átomo
Up: O átomo de Hidrogênio
Previous: Determinando o comportamento assintótico
Henrique Fleming
2003-03-30
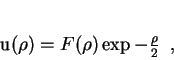

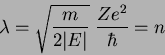
![\begin{eqnarray*}
A_1 l(l+1) & = & 0\\
\left[2 - l(l+1)\right]A_2 = (\lambda -1)A_1
\end{eqnarray*}](img562.png)
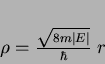
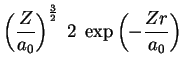
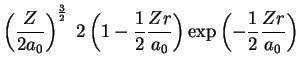
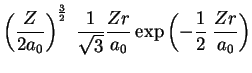
![$\displaystyle \left(\frac{Z}{3a_0}\right)^{\frac{3}{2}}\;2\left[1-\frac{2}{3}\f...
...(\frac{Zr}{a_0}\right)^2\right]
\exp{\left(-\frac{1}{3}\;\frac{Zr}{a_0}\right)}$](img595.png)