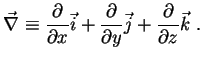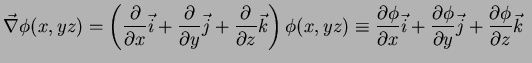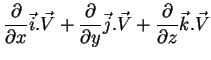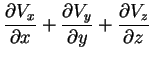Next: Exemplos e exercícios
Up: Campos vetoriais for the
Previous: Introdução
Considere a expressão
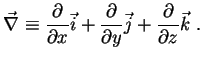 |
(2) |
Como vimos, o gradiente de um campo escalar
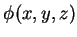 pode ser
escrito como
pode ser
escrito como
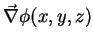 , entendendo-se esta
notação como
, entendendo-se esta
notação como
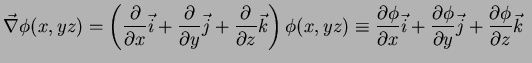 |
(3) |
Seja agora
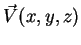 um campo vetorial, e considere a
expressão
um campo vetorial, e considere a
expressão
cujo resultado é um campo escalar. Este campo escalar,
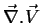 , é denominado ``divergente de
, é denominado ``divergente de 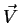 '', e,
veremos, tem também uma grande importância na descrição
física (e matemática) dos campos vetoriais.
'', e,
veremos, tem também uma grande importância na descrição
física (e matemática) dos campos vetoriais.
Subsections
Henrique Fleming
2003-08-11