Um campo vetorial é uma função que associa, a cada ponto do espaço, um vetor. O exemplo mais concreto e elementar é o campo de velocidades de um fluido1. Um fluido é um meio contínuo, e isto se reflete na variação contínua dos valores da velocidade, quando se percorre o fluido.
Matematicamente, um campo vetorial é uma função
Na expressão acima, o
![]() do lado direito é considerado
como o espaço vetorial usual construído sobre o conjunto
do lado direito é considerado
como o espaço vetorial usual construído sobre o conjunto
![]() . Então, a cada ponto do espaço, dado por três
coordenadas, associa-se uma outra terna de números, que são as
componentes de um vetor numa base dada. Uma função como a
descrita acima, denotada mais simplesmente por
. Então, a cada ponto do espaço, dado por três
coordenadas, associa-se uma outra terna de números, que são as
componentes de um vetor numa base dada. Uma função como a
descrita acima, denotada mais simplesmente por
![]() , pode
ser escrita como uma terna de funções
, pode
ser escrita como uma terna de funções
![]() . Diz-se que
. Diz-se que ![]() é contínua
e diferenciável quando cada uma das três componentes,
é contínua
e diferenciável quando cada uma das três componentes,
![]() ,
,
![]() ,
,
![]() for contínua e
diferenciável. Como estas funções são funções de
for contínua e
diferenciável. Como estas funções são funções de
![]() , suas continuidade e
diferenciabilidade já foram definidas e descritas em
``Diferenciabilidade for the practical man''.
, suas continuidade e
diferenciabilidade já foram definidas e descritas em
``Diferenciabilidade for the practical man''.
Resumindo, um campo vetorial é uma função que associa a cada ponto um vetor, cujas componentes variam, de ponto para ponto, de maneira contínua e diferenciável. Isto significa que podemos calcular as derivadas parciais dessas componentes, obtendo novas funções contínuas. Um campo vetorial constante, ou seja, que associa a cada ponto do espaço o mesmo vetor, é chamado, entre os físicos, de campo uniforme. Entre os físicos prefere-se usar o termo campo constante para um campo cujos valores (ou seja, cujos vetores) independem do tempo. Portanto, quando se falar em campo constante, é necessário explicar-se.
A descrição de um fluido utiliza também campos escalares. Estes são, simplesmente funções
Seja
![]() um campo escalar. Podemos calcular o seu gradiente,
um campo escalar. Podemos calcular o seu gradiente,
![]() , e temos
, e temos
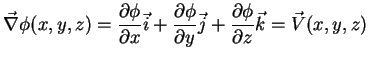 |
(1) |