


Next: Rotações no plano e
Up: O operador diferencial
Previous: Exemplos e exercícios
Para entender por que certas combinações de derivadas, como o
divergente de um vetor, e o laplaceano de um escalar, são
importantes, é conveniente estudar um pouco o que acontece com um
vetor, e quantidades relacionadas a ele, quando se executa uma
rotação no sistema de eixos, passando de um triedro ortogonal a
outro. Na natureza não existem eixos, de maneira que qualquer base
que se utilize na descrição de quantidades físicas, só
pode ter um papel auxiliar, assim como o andaime auxilia na
construção de um prédio, mas é desnecessário para
descrever as propriedades do prédio. Deve-se, por isso, esperar que
as quantidades de real significado físico independam da escolha
de eixo de coordenadas, ou dependam dela de uma maneira muito simples.
Vamos iniciar por rotações muito simples: rotações planas.
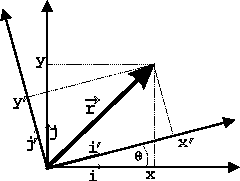
A figura abaixo mostra um sistema de eixos no plano, formada por eixos
nas direções dos vetores unitários 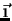 e
e 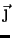 ,
ortogonais. O vetor
,
ortogonais. O vetor 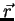 tem, nesses eixos, as componentes
tem, nesses eixos, as componentes 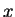 e
e
 , exibidas na figura. Passamos agora dos eixos iniciais para um
novo sistema, girado em relação ao primeiro de um ângulo
, exibidas na figura. Passamos agora dos eixos iniciais para um
novo sistema, girado em relação ao primeiro de um ângulo
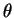 . Os novos eixos são nas direções dadas pelos vetores
. Os novos eixos são nas direções dadas pelos vetores
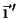 e
e
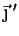 , e são também ortogonais.
As componentes de
, e são também ortogonais.
As componentes de 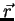 em relação aos novos eixos são
em relação aos novos eixos são
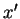 e
e
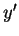 , mostradas na figura.
, mostradas na figura.
Vamos estabelecer as relações entre as componentes do vetor
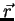 no primeiro e no segundo sistemas de eixo. Elas são
comumente chamadas de fórmulas de transformação das
componentes de um vetor.
no primeiro e no segundo sistemas de eixo. Elas são
comumente chamadas de fórmulas de transformação das
componentes de um vetor.
Embora seja possível obter essas fórmulas diretamente da
figura, vamos dar aqui uma dedução algébrica detalhada. O
vetor 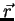 pode ser expandido na base formada pelos vetores
pode ser expandido na base formada pelos vetores
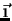 e
e 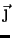 , dando
, dando
 |
(11) |
Pode também ser expandido na base formada por
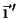 e
e
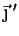 , dando
, dando
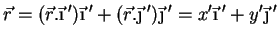 |
(12) |
Por outro lado, os vetores 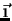 e
e 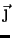 podem ser
expandidos na base formada por
podem ser
expandidos na base formada por
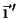 e
e
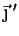 , obtendo-se
, obtendo-se
Usando estes resultados em (11) temos, com (12),
duas expressões para 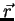 na base (
na base (
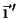 ,
,
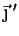 ).
Igualando os coeficientes, obtemos
).
Igualando os coeficientes, obtemos
Note-se que 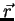 é um vetor que não tem nada de especial. Por isso, seja
é um vetor que não tem nada de especial. Por isso, seja
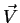 um vetor qualquer, e sejam (
um vetor qualquer, e sejam (
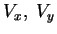 ) suas componentes na base
(
) suas componentes na base
(
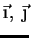 ) e (
) e (
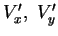 ) suas componentes
na base (
) suas componentes
na base (
 ). Temos
). Temos
As rotações têm uma propriedade especial que simplifica muito seu estudo:
são transformações contínuas. Isto quer dizer que uma rotação de um ângulo
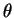 finito, pode ser realizada por uma sucessão de um número enorme de
rotações muito pequenas, até mesmo infinitesimais. Muitas vezes, para provar uma determinada
propriedade das rotações, é suficiente prová-la, então, para rotações
infinitesimais. Vamos usar esta técnica primeiro para o caso que já estudamos,
rotações no plano. Depois, vamos, utilizando de novo esta técnica, passar ao
estudo das rotações infinitesimais em três dimensões.
finito, pode ser realizada por uma sucessão de um número enorme de
rotações muito pequenas, até mesmo infinitesimais. Muitas vezes, para provar uma determinada
propriedade das rotações, é suficiente prová-la, então, para rotações
infinitesimais. Vamos usar esta técnica primeiro para o caso que já estudamos,
rotações no plano. Depois, vamos, utilizando de novo esta técnica, passar ao
estudo das rotações infinitesimais em três dimensões.
Na eq.(15), tomemos o caso em que 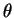 é muito pequeno. Neste caso,
é muito pequeno. Neste caso,
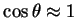 , e
, e
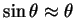 , de maneira que
se obtém
, de maneira que
se obtém
Estas são as propriedades de transformação do vetor 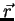 sob uma
rotação infinitesimal.
sob uma
rotação infinitesimal.
Subsections



Next: Rotações no plano e
Up: O operador diferencial
Previous: Exemplos e exercícios
Henrique Fleming
2003-08-11
![]() e
e ![]() ,
ortogonais. O vetor
,
ortogonais. O vetor ![]() tem, nesses eixos, as componentes
tem, nesses eixos, as componentes ![]() e
e
![]() , exibidas na figura. Passamos agora dos eixos iniciais para um
novo sistema, girado em relação ao primeiro de um ângulo
, exibidas na figura. Passamos agora dos eixos iniciais para um
novo sistema, girado em relação ao primeiro de um ângulo
![]() . Os novos eixos são nas direções dadas pelos vetores
. Os novos eixos são nas direções dadas pelos vetores
![]() e
e
![]() , e são também ortogonais.
As componentes de
, e são também ortogonais.
As componentes de ![]() em relação aos novos eixos são
em relação aos novos eixos são
![]() e
e
![]() , mostradas na figura.
, mostradas na figura.
![]() pode ser expandido na base formada pelos vetores
pode ser expandido na base formada pelos vetores
![]() e
e ![]() , dando
, dando
![]() é muito pequeno. Neste caso,
é muito pequeno. Neste caso,
![]() , e
, e
![]() , de maneira que
se obtém
, de maneira que
se obtém