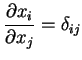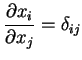Next: O rotacional
Up: O operador diferencial
Previous: Adeus às somatórias
Prove que:
(1)
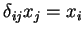
(2)
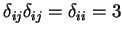
(3) Seja
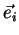 o vetor unitário ao longo do eixo
o vetor unitário ao longo do eixo 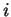 ,
de modo que
,
de modo que
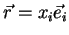 . Mostre que:
. Mostre que:
(a)
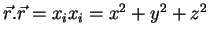
(b) Sejam 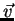 um vetor de componentes
um vetor de componentes 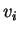 e
e 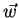 um vetor
de componentes
um vetor
de componentes 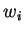 . Então,
. Então,
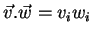 .
.
(c)Considere a função 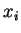 , que a cada ponto associa o valor
da i-ésima coordenada do ponto, e seja
, que a cada ponto associa o valor
da i-ésima coordenada do ponto, e seja 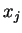 a função análoga
em relação à coordenada
a função análoga
em relação à coordenada 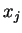 . Então,
. Então,
(4) Seja
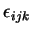 definido assim:
definido assim:
todos os outros valores sendo nulos.
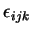 é,
portanto, antissimétrico em todos os índices. Mostre que:
é,
portanto, antissimétrico em todos os índices. Mostre que:
(a)
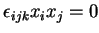
(b)
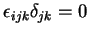
(c)Considere a matriz 3x3 de elementos 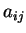 , e seja
, e seja
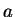 o determinante dessa matriz. Então,
o determinante dessa matriz. Então,
Henrique Fleming
2003-08-11