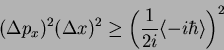Next: A relação de incerteza
Up: Mecânica Quântica
Previous: Algumas propriedades do átomo
Nesta seção vamos apresentar um tratamento formal do princípio da
incerteza, e deduzir as famosas desigualdades de Heisenberg. A
mais famosa delas é:
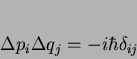 |
(182) |
Em todo espaço dotado de um produto escalar, vale a desigualdade
de Cauchy-Schwartz, que diz que
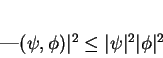 |
(183) |
ou, mais explicitamente,
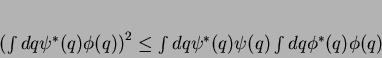 |
(184) |
Seja 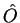 um operador hermiteano, e
um operador hermiteano, e 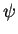 um estado do
sistema. Considere o operador
um estado do
sistema. Considere o operador
onde
Chama-se desvio padrão de 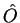 no estado
no estado 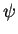 o
número
o
número
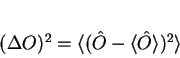 |
(185) |
Entre os físicos, 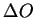 é denominada incerteza de
é denominada incerteza de
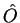 no estado
no estado 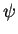 . Sejam
. Sejam 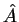 e
e 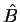 operadores
hermiteanos, e
operadores
hermiteanos, e
dois estados.
É imediato verificar que
Pela desigualdade de Cauchy-Schwartz, temos
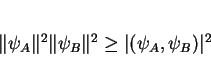 |
(190) |
Por outro lado, para qualquer complexo 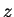 , temos
, temos
Logo,
Ora,
Segue imediatamente que
![\begin{displaymath}
(\psi_{A},\psi_{B})-(\psi_{B},\psi_{A})=\left(\psi,[\hat{A},\hat{B}]\psi\right)
\end{displaymath}](img648.png) |
(191) |
e, da Eq.(191), que
![\begin{displaymath}
\Vert\psi_{A}\Vert^2 \Vert\psi_{B}\Vert^2 \geq
\left(\frac{1}{2i}\rangle[\hat{A},\hat{B}]\rangle \right)^2
\end{displaymath}](img649.png) |
(192) |
ou, em notação mais familiar,
![\begin{displaymath}
(\Delta A)^2(\Delta B)^2 \geq \left(\frac{1}{2i}\langle
[\hat{A},\hat{B}]\rangle\right)^2
\end{displaymath}](img650.png) |
(193) |
que são as relações de incerteza de Heisenberg.
Exemplo: seja
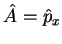 , e
, e
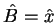 .
Então,
.
Então,
e, finalmente,
Exercício: determine 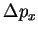 e
e 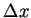 para o estado fundamental do átomo de hidrogênio. Mostre que:
para o estado fundamental do átomo de hidrogênio. Mostre que:
(a)
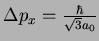 .
.
(b)
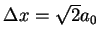 .
.
(c)
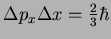
(d) Conclua que o movimento do elétron é 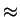 o mínimo
possível compatível com as relações de incerteza.
o mínimo
possível compatível com as relações de incerteza.
Subsections



Next: A relação de incerteza
Up: Mecânica Quântica
Previous: Algumas propriedades do átomo
Henrique Fleming
2003-03-30
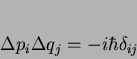
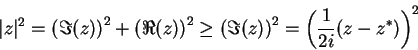
![\begin{displaymath}
\vert(\psi_{A},\psi_{B})\vert^2 \geq
\left(\frac{1}{2i}\left[(\psi_{A},\psi_{B})-(\psi_{B},\psi_{A})\right]\right)^2
\end{displaymath}](img645.png)