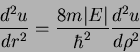Next: Determinando o comportamento assintótico
Up: Mecânica Quântica
Previous: Potenciais com simetria central
O núcleo do átomo de hidrogênio é cerca de 2000 vezes mais pesado
do que um elétron. Por isso se pode ignorar o movimento do núcleo
e descrever o átomo simplesmente como um elétron movendo-se com
energia potencial
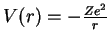 . A Eq.(135) é
então escrita
. A Eq.(135) é
então escrita
![\begin{displaymath}
-\frac{\hbar^2}{2m}\frac{d^2u}{dr^2}+\left[\frac{\hbar^2 l(l+1)} {
2mr^2} -\frac{Ze^2}{r}\right]u(r)=Eu(r)
\end{displaymath}](img514.png) |
(136) |
Note-se que esta equação descreve mais do que o átomo de
hidrogênio: a interação de um elétron com um campo coulombiano
possui também casos em que o elétron não permanece nas
proximidades do núcleo, mas afasta-se indefinidamente dele:
trata-se do espalhamento de um elétron por um campo coulombiano.
Aqui vamos estudar apenas os estados ligados do
elétron: aqueles em que ele está preso ao núcleo, formando um
átomo. O que caracteriza esses estados, na Eq.(136), é
que eles possuem energia negativa. Portanto,
estudaremos as soluções do problema de autovalores dado pela
Eq.(136), com 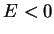 , e, portanto,
, e, portanto, 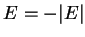 .
É conveniente introduzir variáveis adimensionais. Substituiremos
.
É conveniente introduzir variáveis adimensionais. Substituiremos
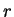 por
por
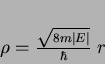 |
(137) |
e a energia, ou, antes, o seu inverso, por
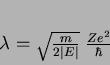 |
(138) |
Deixamos ao leitor a tarefa de verificar que, efetivamente, 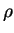 e
e 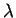 são quantidades adimensionais. Verifica-se facilmente
que
são quantidades adimensionais. Verifica-se facilmente
que
e que a Eq.(136) pode ser reescrita como
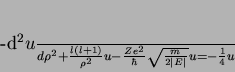 |
(139) |
ou, finalmente,
![\begin{displaymath}
\frac{d^2 u}{d\rho ^2}-\frac{l(l+1)}{\rho ^2}u +
\left[\frac{\lambda}{\rho}-\frac{1}{4}\right]u=0
\end{displaymath}](img523.png) |
(140) |
Resolver este problema de autovalores consiste em determinar os
pares 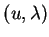 submetidos à condição de que
submetidos à condição de que
que corresponde ao fato de que o átomo tem dimensões finitas.
Para resolver este problema utilizaremos uma técnica devida a
Sommerfeld. Em primeiro lugar, estudaremos que tipos de
comportamento assintótico, para 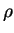 grande, as soluções de
Eq.(140) podem ter. Note-se que a equação
grande, as soluções de
Eq.(140) podem ter. Note-se que a equação
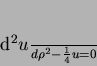 |
(141) |
coincide com a Eq.(140) para grandes valores de 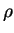 .
Podemos, portanto, afirmar que as soluções de Eq.(141)
devem coincidir com o limite, para grandes
.
Podemos, portanto, afirmar que as soluções de Eq.(141)
devem coincidir com o limite, para grandes 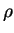 , das soluções da
Eq.(140).
, das soluções da
Eq.(140).
Subsections



Next: Determinando o comportamento assintótico
Up: Mecânica Quântica
Previous: Potenciais com simetria central
Henrique Fleming
2003-03-30
![\begin{displaymath}
-\frac{\hbar^2}{2m}\frac{d^2u}{dr^2}+\left[\frac{\hbar^2 l(l+1)} {
2mr^2} -\frac{Ze^2}{r}\right]u(r)=Eu(r)
\end{displaymath}](img514.png)