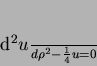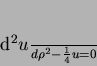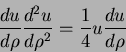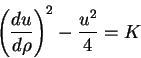Next: As soluções da equação
Up: O átomo de Hidrogênio
Previous: O átomo de Hidrogênio
Considere a equação
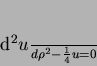 |
(142) |
e vamos multiplicar cada um de seus termos por
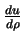 ,
obtendo
,
obtendo
O leitor verificará facilmente que esta equação é a mesma que
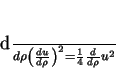 |
(143) |
ou
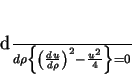 |
(144) |
Portanto,
onde 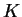 é uma constante. Mas tanto
é uma constante. Mas tanto 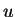 quanto as suas derivadas
tendem a zero no infinito. Logo, a constante
quanto as suas derivadas
tendem a zero no infinito. Logo, a constante 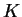 deve ser nula,
pois, calculada no infinito é nula, e tem o mesmo valor em todos
os pontos. Conseqüentemente,
deve ser nula,
pois, calculada no infinito é nula, e tem o mesmo valor em todos
os pontos. Conseqüentemente,
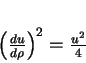 |
(145) |
e
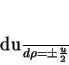 |
(146) |
As soluções dessas equações são
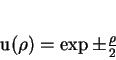 |
(147) |
das quais a que satisfaz os requisitos físicos de se anular no
infinito é
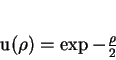 |
(148) |
Este é, então, o comportamento assintótico que as soluções da
Eq.(140) devem ter.



Next: As soluções da equação
Up: O átomo de Hidrogênio
Previous: O átomo de Hidrogênio
Henrique Fleming
2003-03-30