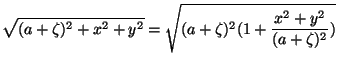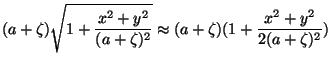Next: A primeira refração
Up: oticag
Previous: Curvatura dos raios de
No tratamento elementar da ótica geométrica obtém-se, por
constrções geométricas utilizando a lei de Snell-Descartes, a
equação
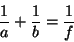 |
(42) |
sendo 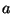 a distância do objeto à lente (supostamente de espessura
desprezíivel),
a distância do objeto à lente (supostamente de espessura
desprezíivel), 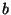 a distância da imagem à lente, e
a distância da imagem à lente, e 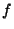 a distância
focal da lente, que é dada por
a distância
focal da lente, que é dada por
sendo 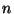 o íindice de refração do vidro,
o íindice de refração do vidro, 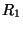 e
e 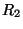 os raios das
superfíicies esféricas da lente. O significado de
os raios das
superfíicies esféricas da lente. O significado de 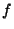 pode ser obtido
facilmente da Eq.(42): tomando-se
pode ser obtido
facilmente da Eq.(42): tomando-se 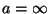 , tem-se
, tem-se
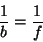 |
(43) |
que mostra ser 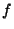 a distância a que se forma a imagem quando o objeto
está no infinito. Na Eq.(42) a lente é suposta de
espessura zero, e a distância à lente é confundida com a distância
ao centro da lente.
a distância a que se forma a imagem quando o objeto
está no infinito. Na Eq.(42) a lente é suposta de
espessura zero, e a distância à lente é confundida com a distância
ao centro da lente.
Vamos tratar esse problema com o uso da equação do eikonal.
Não haverá qualquer dificuldade em tratar o caso de lentes
espessas, e o caminho estará aberto também para o tratamento
de lentes cujas faces não sejam superfícies esféricas.
O ponto 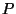 da figura designa a posição do objeto, de
coordenadas
da figura designa a posição do objeto, de
coordenadas 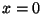 ,
, 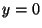 e
e 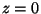 . O eixo
. O eixo 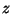 é a direção
de incidência: é a reta que une
é a direção
de incidência: é a reta que une 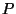 ao centro da lente,
ao centro da lente, 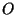 .
.
Um raio partido de 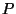 e incidente sobre a lente, encontra-a no
ponto
e incidente sobre a lente, encontra-a no
ponto 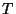 , pertencente a uma superfície esférica de raio
, pertencente a uma superfície esférica de raio
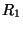 (a primeira face da lente). O centro dessa superfície
esférica está no ponto de coordenadas
(a primeira face da lente). O centro dessa superfície
esférica está no ponto de coordenadas 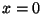 ,
, 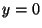 ,
, 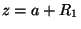 .
As coordenadas de
.
As coordenadas de 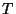 são
são 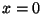 ,
, 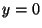 ,
, 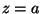 . Um ponto vizinho
à lente tem coordenada
. Um ponto vizinho
à lente tem coordenada 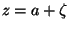 , com
, com 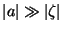 As ondas esféricas emitidas de
As ondas esféricas emitidas de 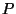 têm o eikonal
têm o eikonal
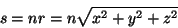 |
(44) |
com 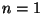 (região externa à lente), ou seja, mais
explicitamente,
(região externa à lente), ou seja, mais
explicitamente,
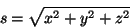 |
(45) |
Perto da primeira face da lente o eikonal é
Restringindo-nos a pequenas aberturas, basta considerar valores
pequenos de 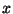 e
e 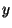 . Então,
. Então,
ou seja,
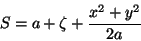 |
(47) |
A equação da superfície da primeira face da lente é
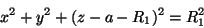 |
(48) |
Podemos agora resolver o problema da primeira refração na
lente.
Subsections



Next: A primeira refração
Up: oticag
Previous: Curvatura dos raios de
Henrique Fleming
2002-04-24
![\begin{picture}(300,100)(0,0)
\CArc(150,75)(50,143,217)
\CArc(70,75)(50,323,37...
...ne(30,90)(172,65){2}
\Vertex(172,75){1}
\PText(172,75)(0)[bl]{B}
\end{picture}](img143.png)
![\begin{picture}(300,100)(0,0)
\PText(60,80)(0)[b]{a}
\CArc(150,75)(50,143,217)...
...xt(100,75)(0)[tr]{T}
\PText(110,75)(0)[bl]{O}
\Vertex(100,75){1}
\end{picture}](img148.png)