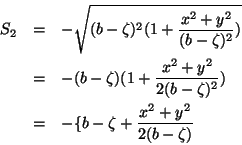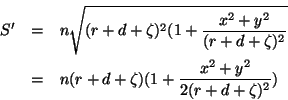Next: A equação dos focos
Up: Lentes esféricas
Previous: A primeira refração
A equação da segunda face, se 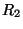 é o seu raio e
é o seu raio e 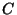 o
seu centro, é
o
seu centro, é
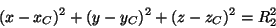 |
(60) |
ou
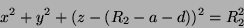 |
(61) |
Para pontos próximos à segunda face, temos
com
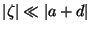 . Então,
. Então,
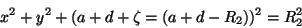 |
(62) |
ou
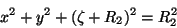 |
(63) |
e, usando o fato de que 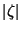 é pequeno,
é pequeno,
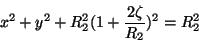 |
(64) |
e, finalmente,
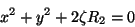 |
(65) |
que podemos por na forma
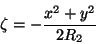 |
(66) |
O eikonal do segundo raio refratado é
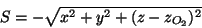 |
(67) |
onde 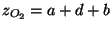 , o que dá
, o que dá
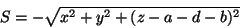 |
(68) |
O sinal (-) é devido ao fato de se tratar de
uma onda esférica que está se contraindo para o ponto 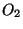 . De fato,
uma onda esférica que sai da origem é
. De fato,
uma onda esférica que sai da origem é
ao passo que uma onda esférica que chega na origem é dada por
Perto da segunda face da lente, temos
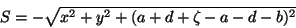 |
(69) |
ou
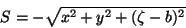 |
(70) |
Para pequenas aberturas,
ou
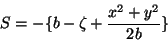 |
(71) |
O eikonal do primeiro raio refratado, quando ele atinge as proximidades
da segunda face da lente, é
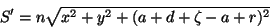 |
(72) |
onde resolvemos denotá-lo por 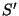 para distinguí-lo do eikonal
do segundo raio refratado. Temos, após uma simplificação,
para distinguí-lo do eikonal
do segundo raio refratado. Temos, após uma simplificação,
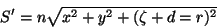 |
(73) |
Para pequenas aberturas,
ou, finalmente,
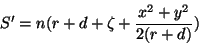 |
(74) |
Devemos então ter, na segunda face,
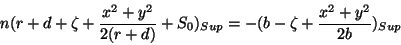 |
(75) |
onde o cálculo deve ser feito para os pontos da segunda superfície da
lente, ou seja, para
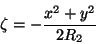 |
(76) |
Temos então
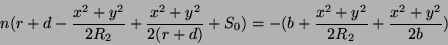 |
(77) |
que dá as equações
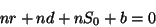 |
(78) |
e
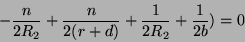 |
(79) |
ou
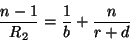 |
(80) |



Next: A equação dos focos
Up: Lentes esféricas
Previous: A primeira refração
Henrique Fleming
2002-04-24
![\begin{picture}(300,100)(0,0)
\CArc(150,75)(50,143,217) \CArc(70,75)(50,323,37)...
...(145,70)(0)[t]{b}\DashLine(70,40)(100,40){2}\PText(65,40)(0)[b]{r}
\end{picture}](img182.png)
![\begin{picture}(300,100)(0,0)
\CArc(150,75)(50,143,217) \CArc(70,75)(50,323,37)...
...(145,70)(0)[t]{b}\DashLine(70,40)(100,40){2}\PText(65,40)(0)[b]{r}
\end{picture}](img182.png)