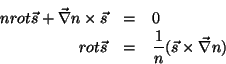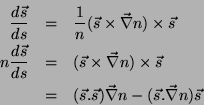Next: Lentes esféricas
Up: oticag
Previous: Simetria esférica
Considere a curva descrita pela extremidade do vetor 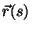 , onde
, onde
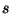 é o comprimento da curva. Seja
é o comprimento da curva. Seja 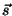 o vetor tangente à curva em
cada ponto. Se a curva for uma reta, a tangente em todos os pontos tem a
mesma direção. Em curvas que não são retas, a tangente ``gira''
quando se percorre a curva. Este movimento da tangente é usado para
definir a curvatura de uma curva como o vetor
o vetor tangente à curva em
cada ponto. Se a curva for uma reta, a tangente em todos os pontos tem a
mesma direção. Em curvas que não são retas, a tangente ``gira''
quando se percorre a curva. Este movimento da tangente é usado para
definir a curvatura de uma curva como o vetor
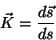 |
(32) |
Como o vetor tangente é
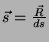 , vemos que a
curvatura é
, vemos que a
curvatura é
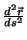 , ou seja é a ``aceleração'',
se
, ou seja é a ``aceleração'',
se 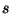 for tomado como o tempo.
for tomado como o tempo.
Considere, por exemplo, um círculo, de equação 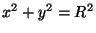 .
Temos
.
Temos
e segue facilmente que
ou,
Como
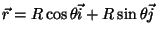 , temos
, temos
que dá
Para a curvatura então temos:
ou
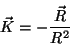 |
(33) |
A curvatura é, então, um vetor, cujo módulo é
A curvatura do círculo é tanto maior quanto menor o raio, o que
mostra que a definição acompanha a idéia intuitiva.
Voltemos ao caso geral. Como o vetor tangente 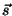 tem módulo
tem módulo 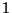 2, de
2, de
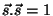 segue que
segue que
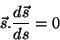 |
(34) |
ou seja,
 é perpendicular a
é perpendicular a 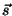 . Logo,
. Logo,
 pode ser escrito na forma
pode ser escrito na forma
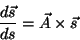 |
(35) |
onde 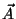 é um vetor a determinar3De fato, considere
o vetor
é um vetor a determinar3De fato, considere
o vetor
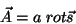 |
(36) |
onde 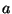 é uma constante. Temos
é uma constante. Temos
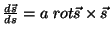 e
e
 |
(37) |
enquanto
e o último termo é nulo, pois
 ,
e
,
e
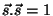 .
Conseqüentemente,
.
Conseqüentemente,
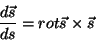 |
(38) |
Até agora falamos genericamente de curvas. Consideremos agora curvas que sejam raios
de luz. Como vimos anteriormente, os raios de luz são ortogonais às superfícies
 , ou seja, têm, em cada ponto dessas superfícies, a direção de
, ou seja, têm, em cada ponto dessas superfícies, a direção de
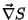 . Em símbolos,
. Em símbolos,
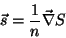 |
(39) |
Daí decorre que
 |
(40) |
onde usamos o fato conhecido 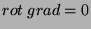 . Da Eq.(40)
segue que
. Da Eq.(40)
segue que
e, portanto, que
e, finalmente,
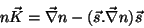 |
(41) |
onde 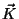 é o vetor curvatura do raio. Uma conseqüência
imediata da Eq.(41) é que em meios homogêneos
(
é o vetor curvatura do raio. Uma conseqüência
imediata da Eq.(41) é que em meios homogêneos
( constante) a curvatura é nula, e os raios são retas. Uma
outra aplicação é a seguinte: quando o Sol está muito
baixo, no nascente ou no poente, os raios que atingem um
observador são aproximadamente horizontais. O índice de
refração da atmosfera diminui com a altitude, logo
constante) a curvatura é nula, e os raios são retas. Uma
outra aplicação é a seguinte: quando o Sol está muito
baixo, no nascente ou no poente, os raios que atingem um
observador são aproximadamente horizontais. O índice de
refração da atmosfera diminui com a altitude, logo
 aponta para o centro da Terra, ou seja, é
vertical. Então, na Eq.(41), o segundo termo do
segundo membro é muito pequeno.
Conclui-se que a curvatura
desses raios é paralela a
aponta para o centro da Terra, ou seja, é
vertical. Então, na Eq.(41), o segundo termo do
segundo membro é muito pequeno.
Conclui-se que a curvatura
desses raios é paralela a
 , apontando para o
centro da Terra. Os raios, isto é, se curvam para baixo. Em
conseqüência, o observador, que interpreta sempre o raio como
uma reta, ``vê'' o Sol mais alto do que está na realidade. De
fato, isto explica por que se vê o Sol ainda um pouco depois de
ele ter se posto.
, apontando para o
centro da Terra. Os raios, isto é, se curvam para baixo. Em
conseqüência, o observador, que interpreta sempre o raio como
uma reta, ``vê'' o Sol mais alto do que está na realidade. De
fato, isto explica por que se vê o Sol ainda um pouco depois de
ele ter se posto.



Next: Lentes esféricas
Up: oticag
Previous: Simetria esférica
Henrique Fleming
2002-04-24