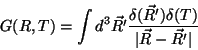Next: Potenciais retardados.
Up: Funções de Green
Previous: Funções de Green
Este estranho nome vem de d'Alembert, grande matemático e enciclopedista francês.
3
Pela definição de função de Green, devemos ter
 |
(16) |
Uma observação crucial: 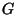 deve ser esfericamente simétrica, uma vez que
é o potencial de uma carga puntiforme que existe só no instante
deve ser esfericamente simétrica, uma vez que
é o potencial de uma carga puntiforme que existe só no instante  . Logo,
. Logo,
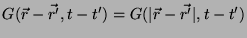 . Vai ser conveniente
introduzir as variáveis
. Vai ser conveniente
introduzir as variáveis
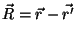 e
e 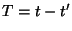 . Pode-se então
dizer que
. Pode-se então
dizer que
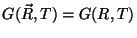 , onde
, onde
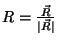 .
.
Aqui introduzimos uma função 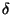 unidimensional,
unidimensional,
 . A definição é a mesma:
. A definição é a mesma:
 exceto
quando
exceto
quando  , sendo infinita neste ponto de tal forma que
, sendo infinita neste ponto de tal forma que
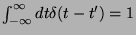 . É um exercício facil
mostrar que
. É um exercício facil
mostrar que
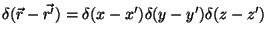 .
.
Para determinar 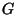 , observemos que, para
, observemos que, para
 ,
a Eq. 16 fica reduzida a
,
a Eq. 16 fica reduzida a
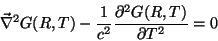 |
(17) |
Para melhor explorar a simetria esférica, passemos a coordenadas esféricas. O
Laplaceano fica então reduzido à parte que contém derivadas em 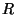 ,
que é 4
,
que é 4
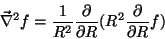 |
(18) |
Portanto, a Eq. 17 se escreve
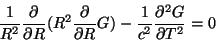 |
(19) |
Vamos introduzir agora a função 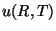 , definida através da relação
, definida através da relação
com 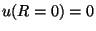 . O leitor verificará facilmente que, em termos de
. O leitor verificará facilmente que, em termos de 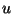 ,
a Eq. 19 se escreve
,
a Eq. 19 se escreve
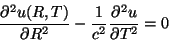 |
(20) |
que é a equação de d'Alembert! Como sabemos, sua solução geral
é
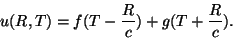 |
(21) |
onde 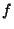 e
e 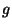 são funções arbitrárias dos argumentos indicados.
Conseqüentemente, a solução geral da Eq. 19
é
são funções arbitrárias dos argumentos indicados.
Conseqüentemente, a solução geral da Eq. 19
é
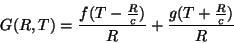 |
(22) |
Isto é o que pode ser obtido considerando apenas o caso
 .
Para obter as expressões detalhadas de
.
Para obter as expressões detalhadas de 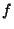 e
e 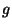 precisaremos estudar o que
ocorre quando
precisaremos estudar o que
ocorre quando
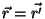 . A função
. A função 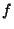 representa uma onda esférica
emergente, de origem em
representa uma onda esférica
emergente, de origem em 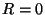 e que nasce em
e que nasce em 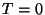 ; em contraposição, a função
; em contraposição, a função
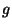 é uma onda esférica incidente, que converge para o ponto
é uma onda esférica incidente, que converge para o ponto 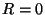 , e o atinge
em
, e o atinge
em 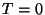 . Ora, estas ondas são conseqüências de uma carga puntiforme que
existiu apenas no instante
. Ora, estas ondas são conseqüências de uma carga puntiforme que
existiu apenas no instante 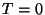 . Logo, a onda incidente, que morre em
. Logo, a onda incidente, que morre em
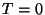 , viola a causalidade, pois existe antes de sua causa. Devemos, portanto,
tomar
, viola a causalidade, pois existe antes de sua causa. Devemos, portanto,
tomar 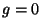 na solução geral.
Na Eq. 16 temos, no primeiro membro, um termo que contém derivadas
nas coordenadas (escondidas sob o símbolo
na solução geral.
Na Eq. 16 temos, no primeiro membro, um termo que contém derivadas
nas coordenadas (escondidas sob o símbolo
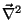 ) e outro que contém
derivadas no tempo. A função de Green é um potencial que se anula no
infinito, e, portanto, tipicamente, uma potência negativa de
) e outro que contém
derivadas no tempo. A função de Green é um potencial que se anula no
infinito, e, portanto, tipicamente, uma potência negativa de
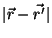 . Por
exemplo,
. Por
exemplo, 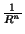 .
Quando se deriva em relação às coordenadas obtém-se, grosso modo,
.
Quando se deriva em relação às coordenadas obtém-se, grosso modo,
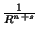 , se se derivou
, se se derivou 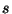 -vezes. O Laplaceano contém derivadas de
segunda ordem, logo, o termo que o contém será da forma
-vezes. O Laplaceano contém derivadas de
segunda ordem, logo, o termo que o contém será da forma
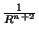 .
Em contraposição, o termo que contém derivadas no tempo não modifica
a dependência com
.
Em contraposição, o termo que contém derivadas no tempo não modifica
a dependência com 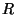 . Assim, depois de calcular os dois termos do primeiro
membro, teremos um da forma
. Assim, depois de calcular os dois termos do primeiro
membro, teremos um da forma
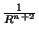 e outro da forma
e outro da forma 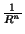 .
Para
.
Para 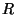 indo a
indo a 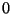 , ou, o que é o mesmo, para
, ou, o que é o mesmo, para 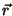 indo a
indo a 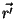 ,
o termo de potência
,
o termo de potência 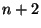 no denominador será muito maior, e podemos desprezar
o outro, frente a ele. Neste limite, então, a equação para a função
de Green será:
no denominador será muito maior, e podemos desprezar
o outro, frente a ele. Neste limite, então, a equação para a função
de Green será:
 |
(23) |
Mas esta é nossa conhecida: é a equação de Poisson! Sua solução
é (copiando cuidadosamente da Eq. 9):
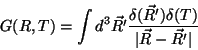 |
(24) |
A integral pode ser facilmente calculada usando a propriedade expressa na
Eq. 3, dando
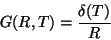 |
(25) |
Mas isto é o limite, para 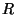 indo a
indo a 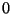 , de
, de
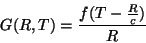 |
(26) |
logo, a função de Green deve ser
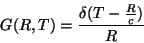 |
(27) |
ou, em todo o detalhe,
 |
(28) |



Next: Potenciais retardados.
Up: Funções de Green
Previous: Funções de Green
Henrique Fleming
2002-04-20