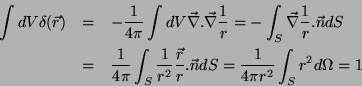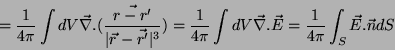Next: Aplicação: solução da equação
Up: Potenciais retardados
Previous: Potenciais retardados
A chamada função delta de Dirac foi introduzida pelo grande Paul Dirac
para simplificar o tratamento de certos problemas da mecânica quântica. Aqui
vamos adaptar o formalismo ao eletromagnetismo. Não se trata de matemática
rigorosa, e sim de uma abreviação, muito intuitiva e eficaz, da teoria das
distribuições de Laurent Schwartz. O feito de Schwartz, que lhe valeu a
medalha Fields (mais ou menos o prêmio Nobel de matemática), foi transformar
as idéias geniais de Dirac em matemática ``politicamente correta'', bem como
ampliar enormemente suas aplicações a outros ramos da matemática, pura
e aplicada.1
Definimos a função delta assim:
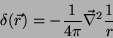 |
(1) |
Em consequência da definição, temos
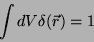 |
(2) |
De fato,
Da definição segue imediatamente que
A mais importante propriedade da 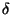 é a seguinte:
é a seguinte:
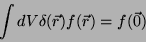 |
(3) |
Demonstração: na primeira integral de 3 , o único valor de
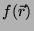 que interessa é
que interessa é 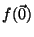 , já que, para qualquer outro valor
de
, já que, para qualquer outro valor
de 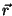 , o produto
, o produto
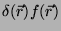 é zero. Logo,
é zero. Logo,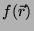 pode ser substituída pela função constante
pode ser substituída pela função constante 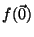 sem mudar o
valor da integral. Então,
sem mudar o
valor da integral. Então,
Mais geralmente, temos:
Uma demonstração quase física da Eq. 6 é obtida
assim:
onde
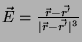 é o
campo elétrico de uma carga unitária localizada em
é o
campo elétrico de uma carga unitária localizada em 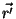 . Logo,
pelo teorema de Gauss,
. Logo,
pelo teorema de Gauss,
Conclui-se, então, que
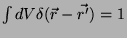 .2
.2



Next: Aplicação: solução da equação
Up: Potenciais retardados
Previous: Potenciais retardados
Henrique Fleming
2002-04-20