


Next: Funções de Green
Up: Potenciais retardados
Previous: A função delta de
No nosso estudo da eletrostática obtivemos a seguinte equação
para o potencial escalar (equação de Poisson):
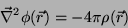 |
(8) |
Usando o princípio de superposição tínhamos a seguinte
expressão para o potencial, em termos da densidade de carga:
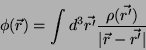 |
(9) |
É intuitivo que 9 seja a solução de
8 (para densidades de carga que tendam a zero a grandes
distâncias). Vamos mostrar agora que isto é efetivamente verdade.
Note-se que, pela definição de
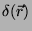 ,
,
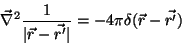 |
(10) |
Vamos mostrar que 9 satisfaz efetivamente a 8.
Aplicando o operador
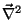 à 9, temos
à 9, temos
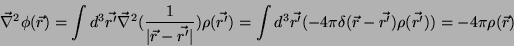 |
(11) |
que é o que se queria provar. Neste cálculo é essencial o fato de
que
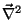 atua somente sobre a variável
atua somente sobre a variável 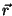 , e não
sobre a
, e não
sobre a 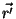 .
.



Next: Funções de Green
Up: Potenciais retardados
Previous: A função delta de
Henrique Fleming
2002-04-20