


Next: A função de Green
Up: Potenciais retardados
Previous: Aplicação: solução da equação
Seja 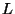 um operador diferencial linear e considere a equação
diferencial
um operador diferencial linear e considere a equação
diferencial
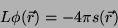 |
(12) |
onde 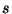 é uma função dada, denominada fonte e
é uma função dada, denominada fonte e 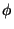 é
a função incógnita. Denomina-se função de Green
do operador linear
é
a função incógnita. Denomina-se função de Green
do operador linear 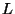 , a função
, a função
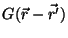 tal que
tal que
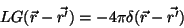 |
(13) |
com condições de contorno definidas pelo particular problema.
Uma vez determinada a função de Green, a Eq. 12 pode ser
resolvida facilmente. De fato, vamos mostrar que
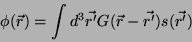 |
(14) |
é solução de 12. Basta aplicar o operador 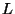 à
14. Temos
à
14. Temos
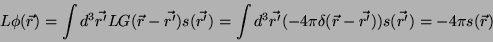 |
(15) |
Para um exemplo, considere o operador linear Laplaceano,
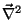 .
Na Eq. 10 lemos que
.
Na Eq. 10 lemos que
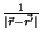 é precisamente
a função de Green. De fato, o método usado acima para construir a solução
da equação de Poisson é exatamente o método da função de Green, que
acabamos de descrever.
é precisamente
a função de Green. De fato, o método usado acima para construir a solução
da equação de Poisson é exatamente o método da função de Green, que
acabamos de descrever.
George Green foi um físico-matemático de primeira grandeza, embora
tenha sido sempre um amador, e nunca tenha tido qualquer diploma universitário. Seu pai
era dono de um moinho, trabalhava duro e achava que esse negócio de física-
matemática era coisa de ...Deixa prá lá! Estudando por conta própria
Green descobriu praticamente todos os métodos matemáticos da teoria de campos, entre
os quais a função de Green e os potenciais 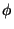 e
e 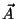 . Publicou, em pequena
tiragem, por conta própria, suas descobertas em um tratado, que se tornou obra
ambicionadíssima e rara, naqueles tempos sem xerox. Quando o jovem William Thomson,
depois Lord Kelvin, visitou Paris, havia uma fila de físicos e matemáticos
eminentes querendo ter uma entrevista com aquele jovem quase desconhecido. O que eles
queriam era tomar emprestado o tratado de Green, do qual Kelvin era o feliz
possuidor de uma cópia.
. Publicou, em pequena
tiragem, por conta própria, suas descobertas em um tratado, que se tornou obra
ambicionadíssima e rara, naqueles tempos sem xerox. Quando o jovem William Thomson,
depois Lord Kelvin, visitou Paris, havia uma fila de físicos e matemáticos
eminentes querendo ter uma entrevista com aquele jovem quase desconhecido. O que eles
queriam era tomar emprestado o tratado de Green, do qual Kelvin era o feliz
possuidor de uma cópia.
Subsections



Next: A função de Green
Up: Potenciais retardados
Previous: Aplicação: solução da equação
Henrique Fleming
2002-04-20