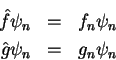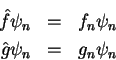Next: Energia e Momento
Up: Operadores
Previous: Valor médio
Sejam 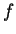 e
e 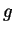 duas quantidades físicas que podem ter valores definidos simultaneamente.
Sejam
duas quantidades físicas que podem ter valores definidos simultaneamente.
Sejam 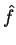 e
e 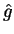 seus operadores. Os autovalores da soma
seus operadores. Os autovalores da soma 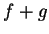 são a soma dos
autovalores de
são a soma dos
autovalores de 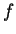 e de
e de 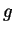 . Considere o operador
. Considere o operador
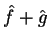 , e sejam
, e sejam 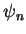 as
autofunções comuns a
as
autofunções comuns a 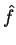 e
e 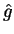 . Então,
. Então,
e, portanto,
Este resultado pode ser generalizado para funções de onda quaisquer, assim:
Neste caso, tem-se
A multiplicação de operadores é definida assim:
Suponhamos que 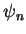 seja autofunção comum a
seja autofunção comum a 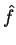 e
e 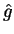 . Então,
. Então,
e
Logo, para as autofunções simultaneas, temos
Isto não é suficiente para se concluir que o operador
Contudo, como o conjunto das autofunções 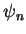 é completo, temos, dada uma função de onda
arbitrária, que
é completo, temos, dada uma função de onda
arbitrária, que
e
Logo, o operador
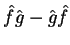 é zero como operador, pois leva qualquer
função ao valor zero. Note-se que isto foi demonstrado para dois operadores que possuem um
conjunto completo de autofunções comuns. No caso geral, esse comutador,
é zero como operador, pois leva qualquer
função ao valor zero. Note-se que isto foi demonstrado para dois operadores que possuem um
conjunto completo de autofunções comuns. No caso geral, esse comutador,
é diferente de zero.



Next: Energia e Momento
Up: Operadores
Previous: Valor médio
Henrique Fleming
2003-03-30