Next: Curvatura dos raios de
Up: Exemplos
Previous: Dois meios homogêneos
Considere a seguinte solução da equação do eikonal, dotada
de simetria esférica:
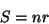 |
(26) |
onde 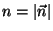 e
e 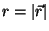 . Temos
. Temos
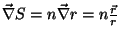 e, portanto,
e, portanto,
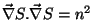 . As
superfícies
. As
superfícies 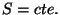 são, neste caso, as superfícies
são, neste caso, as superfícies 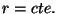 ,
ou seja, as frentes de onda são superfícies esféricas com centro
na origem. Para que se trate verdadeiramente de uma solução da equação
do eikonal, é preciso ainda que a Eq.(16) seja satisfeita:
,
ou seja, as frentes de onda são superfícies esféricas com centro
na origem. Para que se trate verdadeiramente de uma solução da equação
do eikonal, é preciso ainda que a Eq.(16) seja satisfeita:
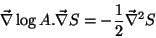 |
(27) |
Ora,
ou
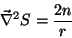 |
(28) |
É necessário então que
ou, que
Segue então que
Portanto,
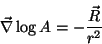 |
(29) |
Mas
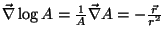 e,
conseqüentemente,
e,
conseqüentemente,
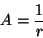 |
(30) |
Podemos então contruir a onda 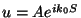 (ver Eq.(6)).
(ver Eq.(6)).
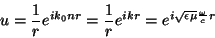 |
(31) |
que é a parte espacial de uma onda esférica.



Next: Curvatura dos raios de
Up: Exemplos
Previous: Dois meios homogêneos
Henrique Fleming
2002-04-24