


Next: Derivadas mistas
Up: Meio
Previous: Coordenadas esféricas
Como aplicação, vamos ao problema de Kepler. Na origem do
sistema de coordenadas está o Sol, de massa 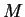 . O vetor
. O vetor 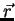 vai do Sol à Terra, de massa
vai do Sol à Terra, de massa 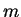 . A força, segundo Newton, é
. A força, segundo Newton, é
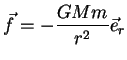 |
(59) |
Como o vetor 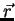 é
é
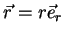 |
(60) |
temos
 |
(61) |
Usando (57),
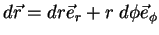 |
(62) |
e, ``dividindo por 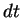 '',
'',
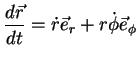 |
(63) |
onde usamos a notação de Newton: o ponto sobre o símbolo
significa sua derivada no tempo.
A derivada segunda de 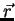 não oferece novas dificuldades.
não oferece novas dificuldades.
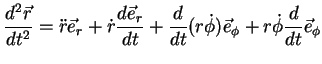 |
(64) |
As derivadas dos vetores de base podem facilmente ser calculadas
usando (57) e (58). Obtemos:
Levando este resultado a (64), obtemos
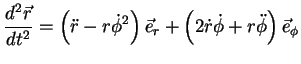 |
(67) |
A lei de Newton assume então a forma:
 |
(68) |
Igualando os coeficientes dos vetores, temos as equações
procuradas:
O prosseguimento em direção à obtenção das
soluções consiste, em primeiro lugar, em notar que,
multiplicando a segunda, termo a termo, por 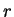 , podemos
reescrevê-la assim:
, podemos
reescrevê-la assim:
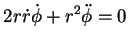 |
(71) |
que é a mesma coisa que
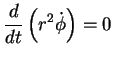 |
(72) |
ou ainda
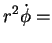 constante constante |
(73) |
Não é dificil identificar esta constante (considerando, por
exemplo, o caso particular de órbita circular): trata-se do
momento angular por unidade de massa. Logo, introduzindo a
notação
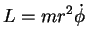 |
(74) |
para o momento angular, podemos escrever
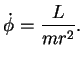 |
(75) |
Inserindo este resultado em (69) e remexendo um pouco,
obtemos a equação
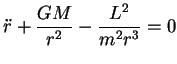 |
(76) |
Resolvendo-se esta equação diferencial para 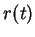 e usando-a
em
e usando-a
em
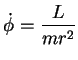 |
(77) |
podemos determinar 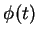 . Isto determina completamente o
movimento.3 Vamos fazer uma análise qualitativa do movimento, usando a equação
(76). Esta equação não contém o ângulo
. Isto determina completamente o
movimento.3 Vamos fazer uma análise qualitativa do movimento, usando a equação
(76). Esta equação não contém o ângulo  . Pode
ser pensada como a equação de movimento como visto por um observador
que gira junto com a Terra, e só percebe o movimento radial. Como não é
um sistema inercial, devemos estar prontos para achar forças de inércia.
. Pode
ser pensada como a equação de movimento como visto por um observador
que gira junto com a Terra, e só percebe o movimento radial. Como não é
um sistema inercial, devemos estar prontos para achar forças de inércia.
De fato, multiplicando (76) por 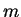 , temos
, temos
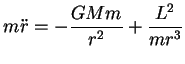 |
(78) |
ou seja, a massa vezes a aceleração (neste sistema a única aceleração
é a radial) é igual à força de Newton mais uma força que é zero se
o momento angular 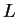 for zero. Esta força é chamada de ```força centrífuga''',
e é uma força de inércia.
for zero. Esta força é chamada de ```força centrífuga''',
e é uma força de inércia.
Multiplicando termo a termo por  , obtemos
, obtemos
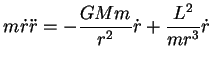 |
(79) |
que pode ser escrita assim:
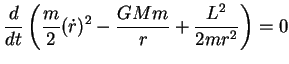 |
(80) |
ou seja,
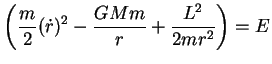 |
(81) |
onde 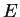 é uma constante. Podemos interpretar esta equação assim:
a energia
é uma constante. Podemos interpretar esta equação assim:
a energia 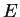 é constituída da energia cinética
é constituída da energia cinética
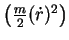 mais a energia potencial, que vem em duas partes: uma atrativa,
mais a energia potencial, que vem em duas partes: uma atrativa,
 e uma repulsiva,
e uma repulsiva,
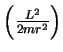 .
Denotando por
.
Denotando por 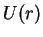 a soma das duas energias potenciais, temos o seguinte gráfico:
a soma das duas energias potenciais, temos o seguinte gráfico:
O movimento só é permitido nas regiões onde
 , do contrário teríamos
energias cinéticas negativas, o que é impossível. Se o planeta tem energia
, do contrário teríamos
energias cinéticas negativas, o que é impossível. Se o planeta tem energia 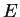 como na figura, seu movimento radial se dá entre os dois pontos em que a linha tracejada
corta a curva de
como na figura, seu movimento radial se dá entre os dois pontos em que a linha tracejada
corta a curva de 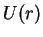 , denotados na figura por
, denotados na figura por 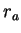 e
e 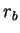 .
Há então um valor máximo e um mínimo de
.
Há então um valor máximo e um mínimo de 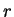 , correspondendo
ao movimento elíptico com o perihélio e o afélio sendo, respectivamente,
, correspondendo
ao movimento elíptico com o perihélio e o afélio sendo, respectivamente,
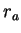 e
e 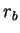 . Notem que, para a reta da energia que tangencia
a curva de de
. Notem que, para a reta da energia que tangencia
a curva de de 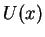 (no seu mínimo), temos um único valor possível
para
(no seu mínimo), temos um único valor possível
para 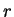 : a órbita é circular. Vemos assim que, para um determinado momento
angular fixo, a órbita de menor energia é a órbita circular.
: a órbita é circular. Vemos assim que, para um determinado momento
angular fixo, a órbita de menor energia é a órbita circular.



Next: Derivadas mistas
Up: Meio
Previous: Coordenadas esféricas
Henrique Fleming
2003-08-11
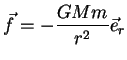
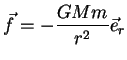
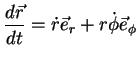
![]() não oferece novas dificuldades.
não oferece novas dificuldades.
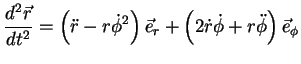

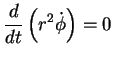
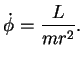
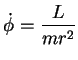
![]() , temos
, temos
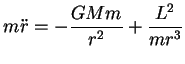
![]() , obtemos
, obtemos
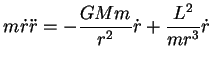
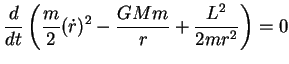
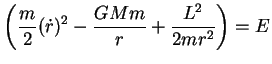
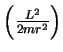 .
Denotando por
.
Denotando por {$r_{a}$}
\uput[0](4.1,1.3){$r_{b}$}
\end{pspicture}](img254.png)
![]() , do contrário teríamos
energias cinéticas negativas, o que é impossível. Se o planeta tem energia
, do contrário teríamos
energias cinéticas negativas, o que é impossível. Se o planeta tem energia ![]() como na figura, seu movimento radial se dá entre os dois pontos em que a linha tracejada
corta a curva de
como na figura, seu movimento radial se dá entre os dois pontos em que a linha tracejada
corta a curva de ![]() , denotados na figura por
, denotados na figura por ![]() e
e ![]() .
Há então um valor máximo e um mínimo de
.
Há então um valor máximo e um mínimo de ![]() , correspondendo
ao movimento elíptico com o perihélio e o afélio sendo, respectivamente,
, correspondendo
ao movimento elíptico com o perihélio e o afélio sendo, respectivamente,
![]() e
e ![]() . Notem que, para a reta da energia que tangencia
a curva de de
. Notem que, para a reta da energia que tangencia
a curva de de ![]() (no seu mínimo), temos um único valor possível
para
(no seu mínimo), temos um único valor possível
para ![]() : a órbita é circular. Vemos assim que, para um determinado momento
angular fixo, a órbita de menor energia é a órbita circular.
: a órbita é circular. Vemos assim que, para um determinado momento
angular fixo, a órbita de menor energia é a órbita circular.