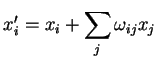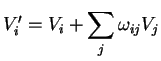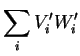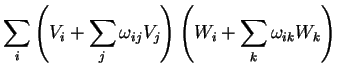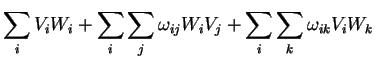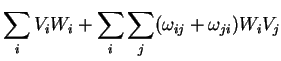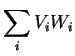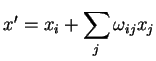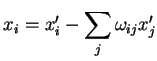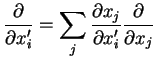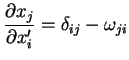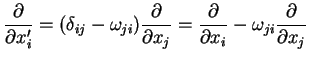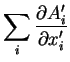Next: Adeus às somatórias
Up: Rotações
Previous: Rotações infinitesimais: parametrização
Uma rotação infinitesimal em três dimensões é definida
como uma transformação linear
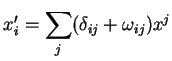 com com 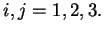 |
(68) |
tal que
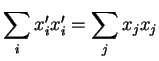 |
(69) |
Também neste caso a condição necessária e suficiente para
que (68) seja uma rotação é que
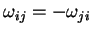 |
(70) |
e o bonito é que a demonstração é exatamente a mesma!
Podem-se usar, passo a passo, as mesmas equações que no caso de
duas dimensões. Melhor, a demostração continua válida para
um número qualquer de dimensões! A única coisa que muda é o
número de valores que os íindices assumem, mas este número
não desempenhou qualquer papel da demonstração.
Para resumir: quando se realiza, sobre o sistema de eixos, uma
rotação infinitesimal, caracterizada pelos parâmetros
infinitesimais
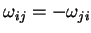 , as coordenadas de um
ponto fixo do espaço se transformam assim:
, as coordenadas de um
ponto fixo do espaço se transformam assim:
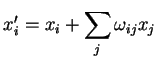 |
(71) |
As componentes de um vetor fixo do espaço, sob esta mesma
rotação, transformam-se assim:
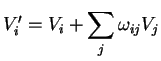 |
(72) |
Exercício: mostrar que o produto escalar de dois vetores é
invariante sob rotações:
Exercício: dada a transformação infinitesimal
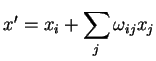 |
(78) |
determinar a transformação inversa.
A inversa é
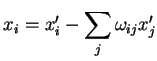 |
(79) |
A verificação é imediata.
Exercício: determinar a transformação nas derivadas
parciais das coordenadas, por uma rotação infinitesimal.
Pela regra da cadeia, temos
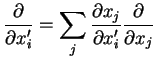 |
(80) |
Como
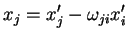 |
(81) |
temos
e, portanto,
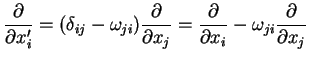 |
(82) |
É conveniente lembrar aqui a fórmula de transformação de um vetor,
sob rotações infinitesimais:
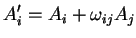 |
(83) |
Vamos agora achar a fórmula de transformação da seguinte quantidade:
A expressão acima não é outra coisa que o divergente de 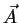 calculado
no referencial em que as coordenadas são
calculado
no referencial em que as coordenadas são
 . Ora,
. Ora,
onde, dentro das regras de tratamento de transformações infinitesimais, desprezamos
termos onde 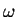 aparecia ao quadrado.
aparecia ao quadrado.
A eq.(84) relata um fato muito importante: o divergente de um campo vetorial
é um invariante: aquela particular combinação de componentes do campo e de derivadas
parciais que o definem num sistema, definem-no em qualquer sistema, e o valor da expressão
é o mesmo. Ou seja, o divergente de um campo vetorial não depende do sistema de coordenadas
utilizado. Pelos nossos argumentos anteriores, temos o direito de esperar que o divergente
de um campo vetorial seja uma quantidade física
importante.4.



Next: Adeus às somatórias
Up: Rotações
Previous: Rotações infinitesimais: parametrização
Henrique Fleming
2003-08-11
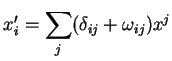 com
com 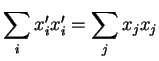
![]() , as coordenadas de um
ponto fixo do espaço se transformam assim:
, as coordenadas de um
ponto fixo do espaço se transformam assim: