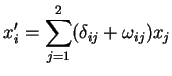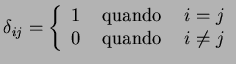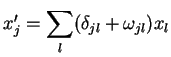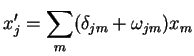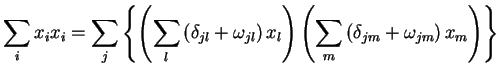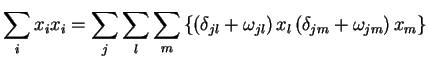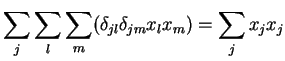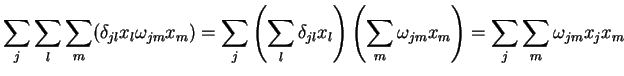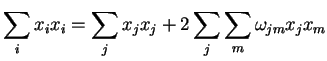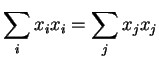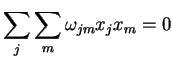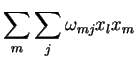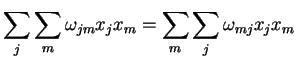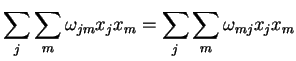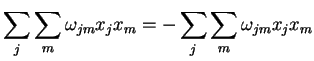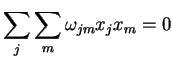Next: Rotações em 3 dimensões
Up: Rotações
Previous: Rotações no plano e
Para sintetizar as fórmulas de transformação
(19), introduzimos a notação indicial, onde
(
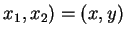 :
:
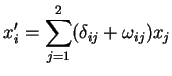 |
(39) |
para 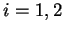 , onde
, onde
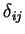 é definido assim
é definido assim
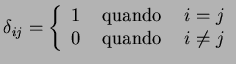 |
(40) |
Expandindo (39), temos
Comparando com (19), vemos que devemos ter
Isto pode ser sintetizado assim:
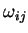 é antissimétrico
(
é antissimétrico
(
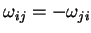 ) e infinitesimal.
) e infinitesimal.
Na realidade, poderíamos chegar a esta conclusão de uma forma
mais geral e rápida: uma rotação é uma transformação
tal que o módulo do vetor girado permanece invariante. Ou seja,
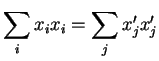 |
(47) |
pois
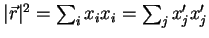 Usando agora a equação (39), vamos eliminar os
Usando agora a equação (39), vamos eliminar os
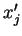 da (47). Escrevemos
para um fator, e
para o outro. A eq.(47) se transforma em
da (47). Escrevemos
para um fator, e
para o outro. A eq.(47) se transforma em
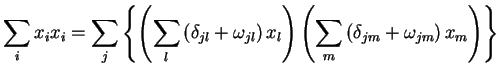 |
(48) |
Como essas somas são associativas, podemos escrever
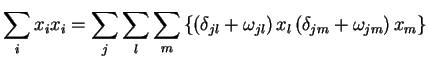 |
(49) |
O termo dentro das somatórias do segundo membro, expandido, dá
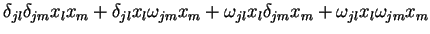 |
(50) |
mas o último termo, que contém o produto de dois 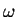 , é
desprezível, pois
, é
desprezível, pois 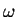 é infinitesimal. Restam, então,
é infinitesimal. Restam, então,
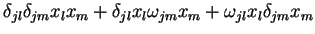 |
(51) |
Vamos calcular termo a termo.
 |
(52) |
Mas
 , e
, e
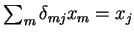 ,
logo,
,
logo,
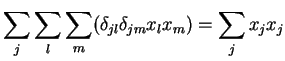 |
(53) |
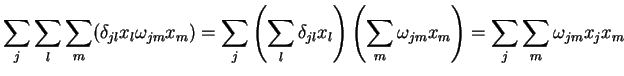 |
(54) |
enquanto que o terceiro termo dá, por motivos análogos,
 |
(55) |
Note-se que a útima soma desta equação pode também ser
escrita
 |
(56) |
pois o nome do índice da soma pode ser qualquer um.
Então, reunindo tudo, temos
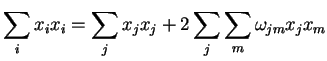 |
(57) |
Como
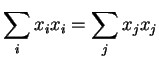 |
(58) |
temos que
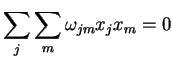 |
(59) |
Qual é a forma mais geral de
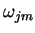 para a qual
esta soma é zero, com
para a qual
esta soma é zero, com 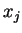 e
e 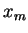 arbitrários?
A resposta é que
arbitrários?
A resposta é que
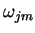 deve ser antissimétrico,
ou seja,
deve ser antissimétrico,
ou seja,
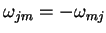 . De fato,
. De fato,
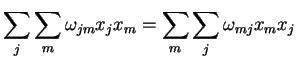 |
(60) |
pois a única coisa que fizemos foi inverter os nomes dos dois
índices. Mas a segunda soma pode também se rescrita
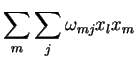 |
(61) |
pois os 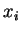 são números. Mas então, podemos reescrever
(60) assim:
são números. Mas então, podemos reescrever
(60) assim:
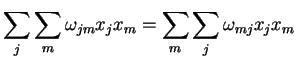 |
(62) |
e, como a ordem das somas é irrelevante, temos
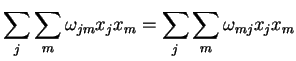 |
(63) |
Se
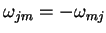 , teremos
, teremos
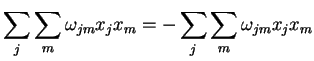 |
(64) |
ou o que é o mesmo,
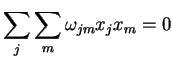 |
(65) |
como se queria demonstrar.
Resumindo, seja a transformação infinitesimal
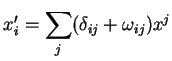 |
(66) |
seja uma rotação, é necessário e suficiente3 que
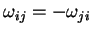 |
(67) |



Next: Rotações em 3 dimensões
Up: Rotações
Previous: Rotações no plano e
Henrique Fleming
2003-08-11