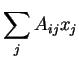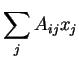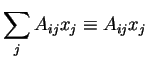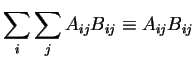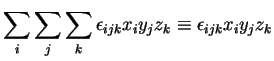Next: Exercícios
Up: Rotações
Previous: Rotações em 3 dimensões
Considere a expressão
que indica uma soma sobre todos os valores do índice 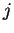 . Note que o índice sobre
o qual se soma,
. Note que o índice sobre
o qual se soma, 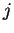 , vem repetido, na expressão. Isto sempre acontece, quando ocorre uma
somatória. Examine o leitor a profusão de somas que foram escritas acima: achará sempre
este fato: quando há uma soma sobre um certo índice, ele aparece repetido na expressão
dentro da somatória. Mas então podemos fazer uma notável economia na notação simplesmente
deixando de escrever o sinal de somatória! (Quem notou isto foi Einstein!). Por exemplo,
na notação que passaremos a usar doravante, chamada convenção de Einstein.
, vem repetido, na expressão. Isto sempre acontece, quando ocorre uma
somatória. Examine o leitor a profusão de somas que foram escritas acima: achará sempre
este fato: quando há uma soma sobre um certo índice, ele aparece repetido na expressão
dentro da somatória. Mas então podemos fazer uma notável economia na notação simplesmente
deixando de escrever o sinal de somatória! (Quem notou isto foi Einstein!). Por exemplo,
na notação que passaremos a usar doravante, chamada convenção de Einstein.
Exemplos:
O leitor atento estará se perguntando: e se eu quiser simplesmente escrever, por exemplo,
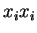 como um símbolo que tem, para
como um símbolo que tem, para 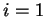 , o valor
, o valor
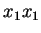 , para
, para
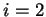 o valor
o valor
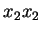 , etc, ou seja, quero expressar um termo da soma, e não a soma?
Neste caso, que é comparativamente raro, convencionamos escrever
, etc, ou seja, quero expressar um termo da soma, e não a soma?
Neste caso, que é comparativamente raro, convencionamos escrever
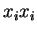
(sem soma)




Next: Exercícios
Up: Rotações
Previous: Rotações em 3 dimensões
Henrique Fleming
2003-08-11