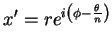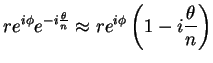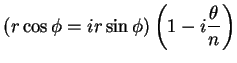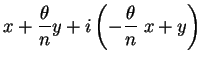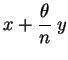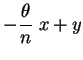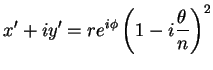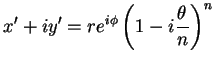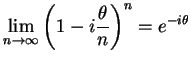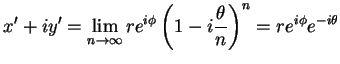Next: Rotações infinitesimais: parametrização
Up: Rotações
Previous: Rotações
A reconstrução de (15) a partir de
(19) não é simples, usando os métodos mais
imediatos. Por isso, vamos, nesta digressão sobre números
complexos, introduzir uma técnica que torna essa tarefa bastante
simples.
Todo número complexo 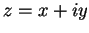 pode ser escrito na representação polar:
pode ser escrito na representação polar:
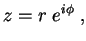 |
(21) |
e a relação entre as duas representações segue facilmente
do uso da famosa fórmula de Gauss:
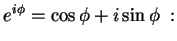 |
(22) |
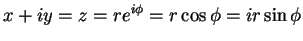 |
(23) |
Executando uma rotação de ângulo 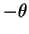 (equivalente a
rodar os eixos de ângulo
(equivalente a
rodar os eixos de ângulo 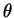 ), temos:
), temos:
Logo,
que reproduz a eq.(15).
Considere agora uma rotação infinitesimal, de ângulo
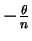 , onde
, onde 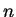 é um inteiro muito grande.
Temos:
é um inteiro muito grande.
Temos:
ou
Então, se realizarmos duas rotações sucessivas de ângulo
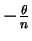 , teremos
, teremos
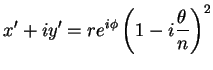 |
(33) |
e, se forem 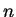 sucessivas,
sucessivas,
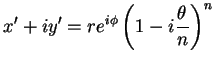 |
(34) |
Como é sabido,
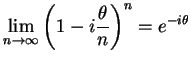 |
(35) |
Logo, no limite de infinitas rotações infinitesimais, temos
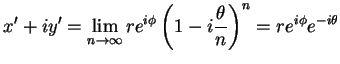 |
(36) |
ou seja, neste limite,
e assim reconstruímos uma rotação finita por uma sucessão
de rotações infinitesimais.
A eficácia do uso de números complexos na descrição de
rotações no plano levou William Rowan Hamilton2 a procurar uma
possível generalização dos números complexos que fizesse
o mesmo para rotações no espaço. Daí nasceram os quaternions.



Next: Rotações infinitesimais: parametrização
Up: Rotações
Previous: Rotações
Henrique Fleming
2003-08-11
![]() pode ser escrito na representação polar:
pode ser escrito na representação polar:
![]() , onde
, onde ![]() é um inteiro muito grande.
Temos:
é um inteiro muito grande.
Temos: