7.1 Definição Dada uma função
![]() , sejam
, sejam ![]() ,...
,...![]() funções reais definidas em
funções reais definidas em
![]() , tais que
, tais que
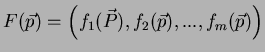
A função ![]() é diferenciável se suas funções
coordenadas o forem. Uma função diferenciável
é diferenciável se suas funções
coordenadas o forem. Uma função diferenciável
![]() é chamada de mapeamento
de
é chamada de mapeamento
de
![]() em
em
![]() . Note que
. Note que
![]() .
.
7.2 Definição Se
![]() é uma curva em
é uma curva em
![]() e
e
![]() é um mapeamento,
então a função composta
é um mapeamento,
então a função composta
![]() é uma curva em
é uma curva em
![]() denominada
imagem de
denominada
imagem de ![]() sob
sob ![]() .
.
7.3 Exemplo
(1) Considere o mapeamento
![]() tal
que
tal
que
Em linhas gerais, o cálculo diferencial aproxima objetos contí
nuos por objetos lineares. Nesta linha, dado um mapeamento
![]() , vamos definir uma aproximação linear para
ele, perto de um ponto
, vamos definir uma aproximação linear para
ele, perto de um ponto
![]() .
.
É possí vel atingir todos os pontos de
![]() através de retas
através de retas
![]() , partindo de
, partindo de ![]() e escolhendo adequadamente
e escolhendo adequadamente
![]() e
e ![]() . Da mesma forma
. Da mesma forma
![]() pode ser ``varrido'' pelas imagens de
pode ser ``varrido'' pelas imagens de
![]() por
por ![]() , ou seja,
, ou seja,
7.4 Definição Seja
![]() um mapeamento.
Seja
um mapeamento.
Seja ![]() um vetor tangente a
um vetor tangente a
![]() em
em ![]() , e denotemos por
, e denotemos por
![]() a velocidade inicial da curva
a velocidade inicial da curva
7.5 Proposição Seja
![]() um
mapeamento de
um
mapeamento de
![]() em
em ![]() . Se
. Se ![]() é um vetor tangente
a
é um vetor tangente
a
![]() em
em ![]() , então
, então
Prova: Vamos tomar ![]() para fixar as idéias. Então
para fixar as idéias. Então
![$\displaystyle \frac{d}{dt}\left(f_i(\vec{p}+tv)\right)_{t=0}=v[f_i]
$](img888.png)
7.6 Corolário Se
![]() é um mapeamento,
então em cada ponto
é um mapeamento,
então em cada ponto ![]() de
de
![]() , o mapeamento tangente
, o mapeamento tangente
7.7 Corolário Seja
![]() um mapeamento. Se
um mapeamento. Se
![]() é a imagem da curva
é a imagem da curva ![]() em
em
![]() , então
, então
![]() .
.
Prova:
![$\displaystyle \alpha^\prime[f_i]=\frac{df_i(\alpha)}{dt}\;,
$](img908.png)

Sejam ![]() ,
,
![]() e
e
![]() ,
,
![]() os referenciais naturais de
os referenciais naturais de
![]() e
e ![]() respectivamente.
Então,
respectivamente.
Então,
7.8 Corolário Se
![]() é um mapeamento
de
é um mapeamento
de
![]() em
em ![]() , então
, então
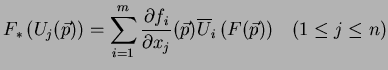
Seja ![]() um espaç o vetorial, com base
um espaç o vetorial, com base ![]() . Seja
. Seja
![]() um outro espaç o vetorial, com base
um outro espaç o vetorial, com base ![]() . Seja
. Seja
![]() linear. Chama-se elementos de matriz de
linear. Chama-se elementos de matriz de ![]() em relação
às bases
em relação
às bases ![]() e
e ![]() os números
os números ![]() na equação
na equação
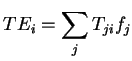
7.9 Definição Um mapeamento
![]() é
regular se, para todo
é
regular se, para todo
![]() , o mapeamento tangente
, o mapeamento tangente
![]() for
for ![]() (injetor).11
(injetor).11
Como mapeamentos tangentes são lineares, segue diretamente da álgebra linear que as seguintes
condições são equivalentes:
(1) ![]() é injetora.
é injetora.
(2)
![]()
(3) A matriz jacobiana de ![]() em
em ![]() tem posto
tem posto ![]() (que é a dimensão
de
(que é a dimensão
de
![]() ).
).
A seguinte propriedade de transformações lineares
![]() será
útil:se os espaç os vetoriais
será
útil:se os espaç os vetoriais ![]() e
e ![]() têm a mesma dimensão, então
têm a mesma dimensão, então
![]() é injetora se e só se ela for sobrejetora.
é injetora se e só se ela for sobrejetora.
Um mapeamento que tem um mapeamento inverso é chamado de difeomorfismo. Lembre-se de que estamos exigindo de um mapeamento que seja diferenciável. Quando considerarmos aplicações mais gerais, um difeomorfismo será uma aplicação diferenciável que possui uma inversa também diferenciável.
7.10 Teorema: Seja
![]() um mapeamento
entre espaç os euclideanos de mesma dimensão. Se
um mapeamento
entre espaç os euclideanos de mesma dimensão. Se ![]() é injetora
em um ponto
é injetora
em um ponto ![]() , existe um aberto
, existe um aberto
![]() contendo
contendo ![]() tal que a restrição de
tal que a restrição de ![]() a
a
![]() é um difeomorfismo de
é um difeomorfismo de
![]() sobre um aberto
sobre um aberto
![]() .
.
Este teorema, de demonstração difí cil, é chamado de teorema da função inversa.
7.11 Definição Funções tangentes.
Seja
![]() um aberto;
um aberto; ![]() um ponto de
um ponto de ![]() e
e
O nome se justifica. Tomemos, para simplificar, o caso em que ![]() . Então
o limite da definição diz que, se
. Então
o limite da definição diz que, se ![]() e
e ![]() são tangentes em
são tangentes em ![]() , teremos,
próximo a
, teremos,
próximo a ![]() ,
,
7.12 Proposição Suponhamos que, dentre as funções tangentes,
em ![]() , à função
, à função ![]() , existam duas funções lineares,
, existam duas funções lineares, ![]() e
e ![]() . Isto
é, suponhamos que
. Isto
é, suponhamos que
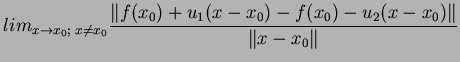 |
0 | ||
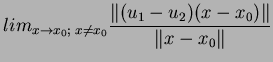 |
0 |


 |
|||
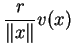 |
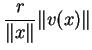 |
|||
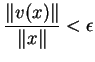
7.14 Definição Dizemos que uma aplicação contínua ![]() de
de
![]() em
em ![]() é diferenciável no ponto
é diferenciável no ponto ![]() se existir
uma aplicação linear
se existir
uma aplicação linear ![]() de
de
![]() tal que
tal que
![]() seja tangente a
seja tangente a ![]() em
em ![]() . Acabamos de ver que esse
mapeamento, quando existe, é único.
. Acabamos de ver que esse
mapeamento, quando existe, é único. ![]() é denominado derivada
de
é denominado derivada
de ![]() no ponto
no ponto ![]() , e é denotado por
, e é denotado por
![]() ou
ou ![]() .
.
Exemplos:
1.A aplicação
![]() , de
, de
![]() é diferenciável.
Por que? Qual é a sua diferencial?
é diferenciável.
Por que? Qual é a sua diferencial?
A função pode ser escrita ![]() . Ela é linear, pois
. Ela é linear, pois
| 0 | |||
| 0 | |||
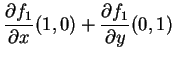 |
|||
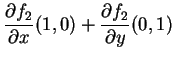 |
7.15 Continuidade de uma aplicação linear
Sejam ![]() e
e ![]() espaços vetoriais com normas definidas e
espaços vetoriais com normas definidas e ![]() uma
aplicação linear de
uma
aplicação linear de ![]() em
em ![]() . Afim de que
. Afim de que ![]() seja contínua, é necessário
e suficiente que exista
seja contínua, é necessário
e suficiente que exista ![]() tal que, para todo
tal que, para todo ![]() ,
,
7.16 Teorema Se a aplicação contínua ![]() de
de
![]() em
em
![]() é diferenciável no ponto
é diferenciável no ponto ![]() , a derivada
, a derivada
![]() é uma aplicação linear
contínua de
é uma aplicação linear
contínua de
![]() .
.
Dem:A continuidade de ![]() significa que, dado
significa que, dado
![]() , existe
, existe
![]() tal que
tal que
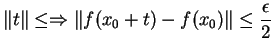
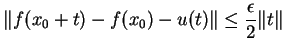
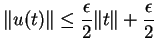

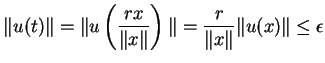
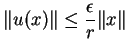
7.17 Teorema A regra da cadeia.
Sejam ![]() ,
,![]() ,
,![]() três espaços vetoriais normados,
três espaços vetoriais normados, ![]() uma vizinhança aberta de
uma vizinhança aberta de ![]() ,
, ![]() uma aplicação contínua de
uma aplicação contínua de ![]() em
em ![]() ,
,
![]() ,
, ![]() uma vizinhança aberta de
uma vizinhança aberta de ![]() em
em ![]() ,
, ![]() uma
aplicação contínua de
uma
aplicação contínua de ![]() em
em ![]() . Então, se
. Então, se ![]() é diferenciável em
é diferenciável em
![]() e
e ![]() é diferenciável em
é diferenciável em ![]() , a aplicação
, a aplicação
![]() é
diferenciável em
é
diferenciável em ![]() , e se tem
, e se tem