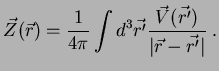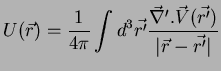Next: Applications
Up: Apêndice: Two theorems by
Previous: Introduction
Actually, the Helmholtz theorem8proves a slightly different thing,
from which the statement above follows immediately: a vector field
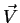 which vanishes at the boundaries can be written as the
sum of two terms, one of which is irrotational and the other,
solenoidal (that is, divergenceless)[12]. Consider the following
well-known identity for an arbitrary vector field
which vanishes at the boundaries can be written as the
sum of two terms, one of which is irrotational and the other,
solenoidal (that is, divergenceless)[12]. Consider the following
well-known identity for an arbitrary vector field
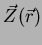 :
:
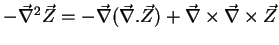 |
(199) |
If we now take our vector field to be
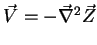 |
(200) |
then it follows that
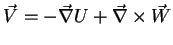 |
(201) |
with
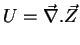 |
(202) |
and
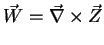 |
(203) |
Eq.(201) is Helmholtz's theorem, as
 is
irrotational and
is
irrotational and
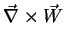 is solenoidal.
is solenoidal.
But, is it general? It assumes that our vector field can be written
as the Laplacian of some other one...
This constitutes, however, no problem
if 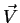 vanishes at infinity fast enough, for, then, the equation
vanishes at infinity fast enough, for, then, the equation
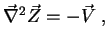 |
(204) |
which is Poisson's equation, has always the solution
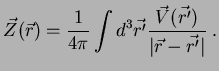 |
(205) |
It is now a simple matter to prove, from Eq.(201), that
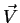 is determined from its
is determined from its 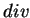 and
and 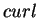 . Taking, in fact, the
divergence of Eq.(201), we have:
. Taking, in fact, the
divergence of Eq.(201), we have:
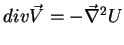 |
(206) |
which is, again, Poisson's equation, and, so, determines 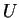 as
as
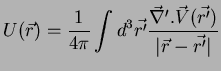 |
(207) |
Take now the 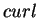 of Eq.(201). We have
of Eq.(201). We have
Now,
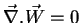 , as
, as
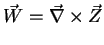 , so
another Poisson equation determines
, so
another Poisson equation determines  . Using
. Using 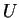 and
and  so
determined
in Eq.(201) proves our contention.
so
determined
in Eq.(201) proves our contention.



Next: Applications
Up: Apêndice: Two theorems by
Previous: Introduction
Henrique Fleming
2003-08-11
![]() vanishes at infinity fast enough, for, then, the equation
vanishes at infinity fast enough, for, then, the equation