


Next: The Second Theorem
Up: Apêndice: Two theorems by
Previous: The First Theorem
We start with a very simple one. Consider a homogeneous, ohmian
conductor, and let
the current density 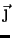 vanish at the closed surface which
encircles it. We
want to inquire as to the possibility that a stationary current may exist
in this
conductor. We then have
vanish at the closed surface which
encircles it. We
want to inquire as to the possibility that a stationary current may exist
in this
conductor. We then have
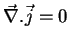 , as the current is
supposed to
be stationary, and
, as the current is
supposed to
be stationary, and
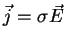 , which is Ohm's law. Also,
, which is Ohm's law. Also,
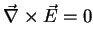 , for a static
, for a static 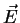 .
But then,
.
But then,
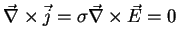 |
(209) |
and so we have both
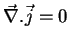 and
and
 .
Besides,
.
Besides, 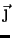 vanishes at the boundaries. It follows, then, from
Helmholtz's theorem, that
vanishes at the boundaries. It follows, then, from
Helmholtz's theorem, that 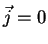 . So, no stationary current can run
under
these conditions. Notice that this is true also for a torus and its
continuous
deformations, so that it applies to any closed circuit, proving the
necessity that the condition
. So, no stationary current can run
under
these conditions. Notice that this is true also for a torus and its
continuous
deformations, so that it applies to any closed circuit, proving the
necessity that the condition
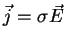 be broken somewhere
in the circuit (where the electromotive force is located).
be broken somewhere
in the circuit (where the electromotive force is located).
Consider now the electromagnetic potentials. The Maxwell equation
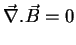 |
(210) |
states that there exists a vector field 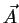 such that
such that
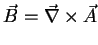 |
(211) |
this 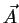 being called the vector potential. We may assume that
being called the vector potential. We may assume that
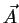 vanishes
at infinity. Now, what we know about
vanishes
at infinity. Now, what we know about 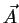 is just its
is just its 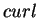 . Therefore,
by Helmholtz's
theorem, we are free to choose the value of its divergence. For instance,
we may
take
. Therefore,
by Helmholtz's
theorem, we are free to choose the value of its divergence. For instance,
we may
take
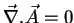 , determining completely
, determining completely 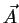 . This is
the so-called
Coulomb gauge. But we can also put
. This is
the so-called
Coulomb gauge. But we can also put
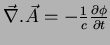 ,
, 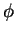 being the scalar potential. This is the Lorentz
gauge.
being the scalar potential. This is the Lorentz
gauge.



Next: The Second Theorem
Up: Apêndice: Two theorems by
Previous: The First Theorem
Henrique Fleming
2003-08-11