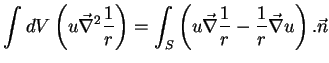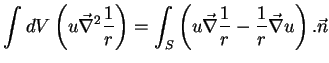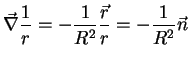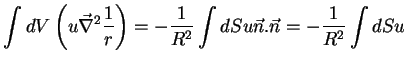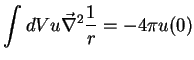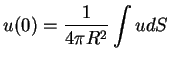Next: Aplicações
Up: A magia da equação
Previous: Teorema de unicidade
Funções harmônicas, e, em particular, potenciais em regiões onde
não há cargas, não podem ter máximos nem mínimos. A
demonstração deste importante resultado é usualmente feita
utilizando a segunda fórmula de Green. Seja 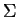 uma
superfície esférica com centro em
uma
superfície esférica com centro em 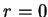 , e
, e 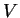 o volume delimitado
por ela. Seja
o volume delimitado
por ela. Seja
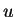 uma função harmônica, e seja
uma função harmônica, e seja
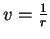 , que é uma
função harmônica exceto para
, que é uma
função harmônica exceto para 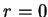 .
A segunda fórmula de Green aplicada a essas funções
.
A segunda fórmula de Green aplicada a essas funções 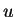 e
e 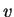 dá:
dá:
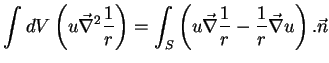 |
(182) |
Mas, na superfície esférica, onde a segunda integral é calculada,
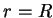 , onde
, onde 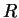 , constante, é o raio da esfera. Logo,
, constante, é o raio da esfera. Logo,
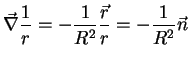 |
(183) |
e, então,
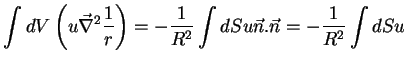 |
(184) |
Mas (veja Apêndice),
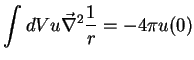 |
(185) |
logo,
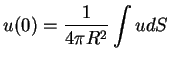 |
(186) |
que está nos dizendo o seguinte: uma função harmônica tem, em
qualquer ponto, como valor, a média dos valores que tem em uma superfície
esférica qualquer centrada neste ponto (desde que contida na região
em que a função é harmônica). Uma aplicação imediate é a seguinte:
dada uma distribuição de cargas em repouso, não há pontos em que
uma carga-teste permaneça em equilíbrio, a não ser aqueles
pontos onde já existam cargas (e, por conseguinte, onde a equação
de Laplace não seja satisfeita).



Next: Aplicações
Up: A magia da equação
Previous: Teorema de unicidade
Henrique Fleming
2003-08-11