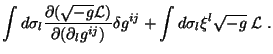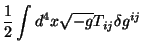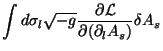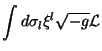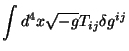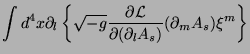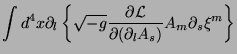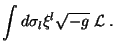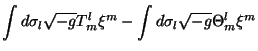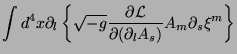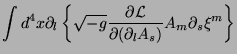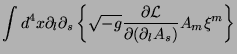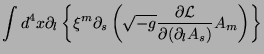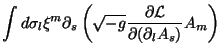Next: Conclusão
Up: O Tensor de Momento-Energia
Previous: Questões de equivalência
Embora mesons escalares sejam simples demais, eles são convenientes
para expor, na forma mais simples, a estratégia da
demonstração. Passemos agora ao caso da Eletrodinâmica, onde
as feições do caso geral já se tornarão claras. Além
disso, as conclusões se aplicarão também ao caso dos mesons
vetoriais.
Considere a equação (3). Ela exibe a variação
de forma de um campo escalar, um ingrediente essencial para a
discussão prévia. A variação de forma de um campo vetorial
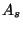 é dada por [6]
é dada por [6]
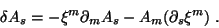 |
(18) |
Isto induz na ação 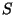 a variação
a variação
Procedendo como antes,
Suponha que a lagrangeana não dependa de
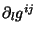 .
Então, usando as equações de movimento para
.
Então, usando as equações de movimento para 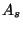 e a
definição do tensor de momento-energia métrico, obtemos
e a
definição do tensor de momento-energia métrico, obtemos
Vamos estudar agora o segundo termo em detalhe. É melhor
escrevê-lo na forma
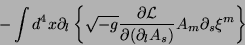 |
(22) |
onde fizemos uso da variação de forma de 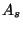 . Levando isto
à equação (3),
. Levando isto
à equação (3),
Transformando a segunda integral numa integral de superfície e
usando (3),
onde usamos
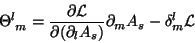 |
(25) |
Assim
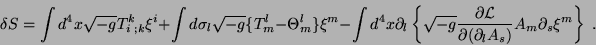 |
(26) |
Usando o fato de que
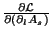 é antissimétrico em
é antissimétrico em
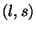 , temos
, temos
Juntamente com com a Eq.(26) isto dá
Isto deve se anular para 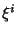 e domínio de integração
arbitrários. Por isso,
e domínio de integração
arbitrários. Por isso,
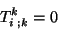 |
(29) |
e a integral de superfície também deve se anular. Em
coordenadas cartesianas 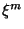 podem ser tomados constantes, e então
segue que
podem ser tomados constantes, e então
segue que
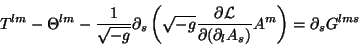 |
(30) |
onde 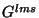 é antissimétrico nos índices
é antissimétrico nos índices 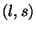 . Ora, o
último termo do primeiro membro tem ele mesmo esta simetria, de
forma que
. Ora, o
último termo do primeiro membro tem ele mesmo esta simetria, de
forma que
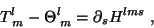 |
(31) |
onde 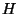 é um novo tensor com as mesmas simetrias de
é um novo tensor com as mesmas simetrias de 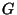 . Logo,
. Logo, 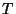 e
e 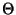 são dois tensores de momento-energia equivalentes (Veja
[1], §32).
são dois tensores de momento-energia equivalentes (Veja
[1], §32).



Next: Conclusão
Up: O Tensor de Momento-Energia
Previous: Questões de equivalência
Henrique Fleming
2002-04-24
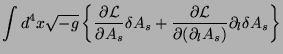
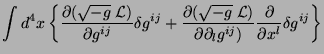
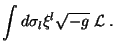
![$\displaystyle \int d^4x\sqrt{-g} \left\{\frac{\partial
\mathcal{L}}{\partial
A_...
...ac{\partial
\mathcal{L}}{\partial(\partial_l A_{s})}\right]\right\}\delta A_{s}$](img47.png)
![$\displaystyle \int d^4 x\left[\frac{\partial\left(\sqrt{-g}\;
\mathcal{L}\right...
...sqrt{-g}\;
\mathcal{L}\right)}{\partial(\partial_l g^{ij})}\right]\delta g^{ij}$](img17.png)
![$\displaystyle \int d\sigma_l\left[\sqrt{-g}\frac{\partial \mathcal{L}
}{\partial(\partial_l \phi)}\right]\delta \phi$](img18.png)