Next: Sumário
Up: O Tensor de Momento-Energia
Previous: Eletrodinâmica
No caso do meson vetorial a demonstração da equivalência fez
uso de dois fatos: o lagrangeano não dependia de
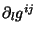 , e
, e
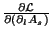 era
antissimétrica em
era
antissimétrica em 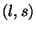 . A última propriedade é comum a todos
os lagrangeanos que descrevem partículas de spin inteiro, no
formalismo de Fierz-Pauli[7]. Para um tratamento breve e
muito lúcido desse formalismo, veja [8]. Em
relação à dependência em
. A última propriedade é comum a todos
os lagrangeanos que descrevem partículas de spin inteiro, no
formalismo de Fierz-Pauli[7]. Para um tratamento breve e
muito lúcido desse formalismo, veja [8]. Em
relação à dependência em
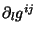 , veremos que
nenhum problema se põe (no caso de haver a dependência) para o
espaço-tempo de Minkowski.
Considere um campo que é um tensor de posto
, veremos que
nenhum problema se põe (no caso de haver a dependência) para o
espaço-tempo de Minkowski.
Considere um campo que é um tensor de posto 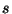 , simétrico em
todos os seus índices, que se anula por contração em
relação a qualquer par de índices, e que satisfaz a
condição de 4-transversalidade,
, simétrico em
todos os seus índices, que se anula por contração em
relação a qualquer par de índices, e que satisfaz a
condição de 4-transversalidade,
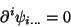 |
(32) |
e seja sua dinâmica descrita pela lagrangeana
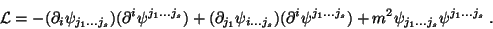 |
(33) |
Este campo representa uma partícula de spin 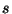 [8] e tem a variação de forma
[8] e tem a variação de forma
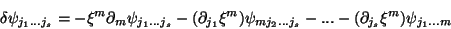 |
(34) |
Note que
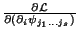 é
antissimétrico em
é
antissimétrico em 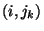 para todo
para todo 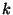 .
Podemos agora reproduzir cada passo da demonstração prévia. O
termo
.
Podemos agora reproduzir cada passo da demonstração prévia. O
termo
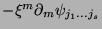 da variação de
forma participará da expressão de
da variação de
forma participará da expressão de
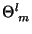 . Os termos
restantes da eq.(34) irão, como na eq.(29), compor
os termos
. Os termos
restantes da eq.(34) irão, como na eq.(29), compor
os termos 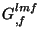 , que serão a soma de
, que serão a soma de 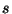 termos, todos com
as mesmas simetrias de índices. Termina-se com a seguinte
expressão:
termos, todos com
as mesmas simetrias de índices. Termina-se com a seguinte
expressão:
Mas o espaço-tempo de Minkowski tem máxima simetria, o que quer
dizer que é possível escolher os 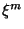 de maneira que
de maneira que
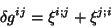 |
(36) |
se anulem, restando uma família a 10 parâmetros de vetores
arbitrários. O anulamento de 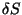 para cada um desses
para cada um desses 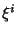 garante, portanto, o resultado
garante, portanto, o resultado
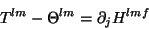 |
(37) |
(onde o 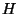 será, em geral, um novo tensor com as mesmas simetrias
de
será, em geral, um novo tensor com as mesmas simetrias
de 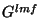 ) mesmo quando o lagrangeano depende de
) mesmo quando o lagrangeano depende de
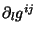 , desde que o espaço-tempo seja de minkowski.
Poderíamos tratar também o caso de spin semi-inteiro, mas seria
necessária a introdução do formalismo de tetradas, o que nos
levaria longe demais. Por enquanto remetemos o leitor a
[9].
, desde que o espaço-tempo seja de minkowski.
Poderíamos tratar também o caso de spin semi-inteiro, mas seria
necessária a introdução do formalismo de tetradas, o que nos
levaria longe demais. Por enquanto remetemos o leitor a
[9].



Next: Sumário
Up: O Tensor de Momento-Energia
Previous: Eletrodinâmica
Henrique Fleming
2002-04-24