Next: Eletrodinâmica
Up: O Tensor de Momento-Energia
Previous: Introdução
Para introduzir apropriadamente o tensor de momento-energia métrico
é preciso que trabalhemos com coordenadas curvilíneas. Seja
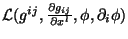 a densidade lagrangeana. A ação é
dada
por
a densidade lagrangeana. A ação é
dada
por
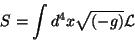 |
(1) |
O tensor de momento-energia métrico é obtido[1]
explorando-se o fato de que 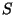 deve ser invariante sob
transformações infinitesimais de coordenadas
deve ser invariante sob
transformações infinitesimais de coordenadas
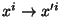 , com
, com
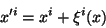 |
(2) |
Os campos e a métrica respondem a essa transformação da
maneira seguinte[1]:
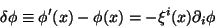 |
(3) |
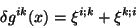 |
(4) |
Isto induz na ação 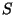 a variação
a variação
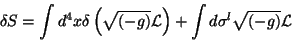 |
(5) |
onde a segunda integral é essencial, uma vez que
uma transformação geral de coordenadas não se anula
necessariamente na fronteira de um domínio de integração.
Para uma bela dedução desse termo, veja ([5]). Trata-se
da sua equação (170). Como veremos, este termo de
superfície é a chave de toda a prova. Mais explicitamente,
As integrações parciais usuais levam a
Quando 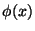 satisfaz as equações de movimento, a primeira
integral se anula. Definindo[1] o tensor de momento-energia
métrico
satisfaz as equações de movimento, a primeira
integral se anula. Definindo[1] o tensor de momento-energia
métrico 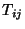 por
por
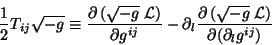 |
(8) |
tem-se
Suponhamos, por um momento, que 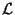 não dependa das
derivadas de
não dependa das
derivadas de 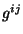 . Isto quer dizer que os coeficientes sda
conexão
. Isto quer dizer que os coeficientes sda
conexão
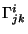 não estrão presentes, explicitamente
ou através dos vários tensores de curvatura. (Naturalmente isto
é sempre verdade no espaço-tempo de Minkowski descrito por
coordenadas ``cartesianas''). Inserindo em (10) os valores
de
não estrão presentes, explicitamente
ou através dos vários tensores de curvatura. (Naturalmente isto
é sempre verdade no espaço-tempo de Minkowski descrito por
coordenadas ``cartesianas''). Inserindo em (10) os valores
de 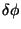 e
e 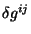 , temos
, temos
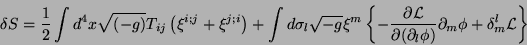 |
(10) |
isto é,
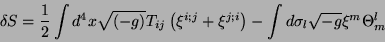 |
(11) |
onde reconhecemos
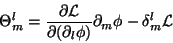 |
(12) |
como o tensor de momento-energia canônico. Ora, como é mostrado em
detalhe na referência ([1]),
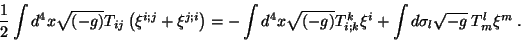 |
(13) |
Levando (13) à (11),
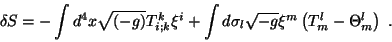 |
(14) |
Como 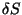 deve se anular para
deve se anular para 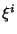 arbitrário, obtém-se
arbitrário, obtém-se
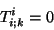 |
(15) |
e
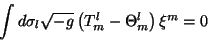 |
(16) |
ou, finalmente,
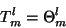 |
(17) |
mostrando a equvalência dos dois tensores.1



Next: Eletrodinâmica
Up: O Tensor de Momento-Energia
Previous: Introdução
Henrique Fleming
2002-04-24
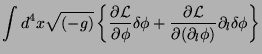
![$\displaystyle \int
d^4x\left[\frac{\partial\left(\sqrt{(-g)}\mathcal{L}\right)}...
...
g^{ij}}{\partial x^l}\right)}\frac{\partial}{\partial x^l}\delta
g^{ij}\right]$](img14.png)
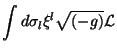
![$\displaystyle \int d^4x \sqrt{(-g)} \left\{\frac{\partial
\mathcal{L}}{\partial...
...\frac{\partial \mathcal{L}}{\partial(\partial_l
\phi)}\right]\right\}\delta\phi$](img16.png)
![$\displaystyle \int d^4 x\left[\frac{\partial\left(\sqrt{-g}\;
\mathcal{L}\right...
...sqrt{-g}\;
\mathcal{L}\right)}{\partial(\partial_l g^{ij})}\right]\delta g^{ij}$](img17.png)
![$\displaystyle \int d\sigma_l\left[\sqrt{-g}\frac{\partial \mathcal{L}
}{\partial(\partial_l \phi)}\right]\delta \phi$](img18.png)