


Next: Questões de equivalência
Up: O Tensor de Momento-Energia
Previous: O Tensor de Momento-Energia
É fato bem conhecido que o tensor de momento-energia
canônico[1] de um campo clássico não é simétrico
pela troca de seus índices, exceto no caso de campos de spin
nulo. Por causa disso ele é substuído usualmente por um outro,
simétrico, que lhe é equivalente enquanto densidade de energia e
momento[2][3].
Uma alternativa possível é o uso do tensor de momento-energia
métrico, introduzido por Hilbert em seu trabalho
clássico[4], onde ele surge como a fonte tensorial
correta para o campo gravitacional.
Assim, os tensores de momento-energia canônico e métrico têm
origens muito diversas, e definições ainda mais diversas. Custa
crer que tenham o mesmo significado físico, isto é, que sejam
equivalentes.
Neste artigo buscamos elucidar de um maneira simples quando é que
essas duas espécies de tensor de momento-energia são de fato
equivalentes. Mais precisamente, calculando-se o tensor métrico e
passando-se ao espaço plano descrito por coordenadas cartesianas,
quando é que se obtém um tensor equivalente ao tensor de
momento-energia canônico? Começaremos pelo caso muito simples de
um campo escalar 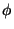 . A seguir trataremos do caso de um meson
vetorial, onde os aspectos gerais do problema já serão
vislumbrados, e esboçaremos uma extensão para outros spins.
O método apresentado aqui tem talvez a vantagem de requerer apenas
uma extensão (bastante natural) daquele usualmente encontrado nos
tratados clássicos[1]. Uma demonstração do mesmo
resultado há de estar contida no tratamento muito geral (e muito
complicado!) da ref.([3]). Não conheço nenhum livro
que trate do assunto: em geral apresentam apenas argumentos de
plausibilidade.
. A seguir trataremos do caso de um meson
vetorial, onde os aspectos gerais do problema já serão
vislumbrados, e esboçaremos uma extensão para outros spins.
O método apresentado aqui tem talvez a vantagem de requerer apenas
uma extensão (bastante natural) daquele usualmente encontrado nos
tratados clássicos[1]. Uma demonstração do mesmo
resultado há de estar contida no tratamento muito geral (e muito
complicado!) da ref.([3]). Não conheço nenhum livro
que trate do assunto: em geral apresentam apenas argumentos de
plausibilidade.



Next: Questões de equivalência
Up: O Tensor de Momento-Energia
Previous: O Tensor de Momento-Energia
Henrique Fleming
2002-04-24