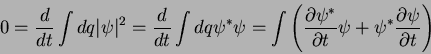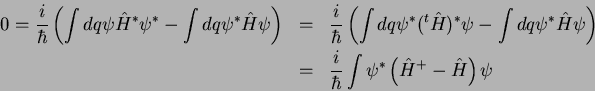Next: O comutador de e
Up: Energia e Momento
Previous: Energia e Momento
Diremos que um operador 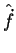 é a derivada no tempo do operador
é a derivada no tempo do operador 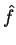 se, sendo
se, sendo
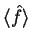 o valor médio de
o valor médio de 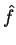 num estado arbitrário, e
num estado arbitrário, e
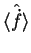 o valor médio de
o valor médio de 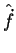 nesse mesmo estado,
tivermos
nesse mesmo estado,
tivermos
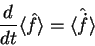 |
(17) |
Explicitando, devemos ter
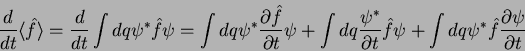 |
(18) |
Usando a equação de Schrödinger, obtemos
Usando esses resultados em (18), temos
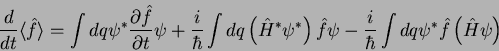 |
(19) |
O termo que contém a derivada parcial do operador só existe quando a expressão
do operador contém parâmetros que dependam do tempo. Por exemplo, se tivéssemos
uma partícula livre de massa variável, seu hamiltoniano seria
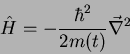 |
(20) |
e a derivada em questão seria dada por
Na grande maioria dos casos este termo é inexistente.
Voltando à Eq.(19), e usando o fato de que 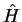 é hermiteano, temos
é hermiteano, temos
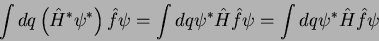 |
(21) |
e, conseqüentemente,
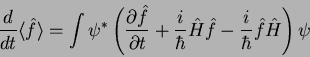 |
(22) |
Como, por definição,
temos que
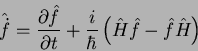 |
(23) |
Como dissemos, o caso mais importante é aquele em que
 (diz-se então que o operador não tem dependência
explícita no tempo.) Neste caso,
(diz-se então que o operador não tem dependência
explícita no tempo.) Neste caso,
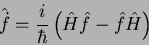 |
(24) |
Vemos então que, se
![$[\hat{H},\hat{f}]=0$](img177.png) ,
,
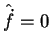 , e
, e
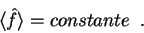 |
(25) |
Na mecânica quântica, a constância de uma quantidade física no tempo quer dizer isto:
que o valor médio dessa quantidade independe do tempo. Considere o operador 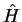 .
Temos, evidentemente, que
.
Temos, evidentemente, que
![$[\hat{H},\hat{H}]=0$](img180.png) , logo, se
, logo, se 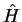 não depende explicitamente
do tempo,
não depende explicitamente
do tempo,
![\begin{displaymath}
\hat{\dot{H}} = \frac{i}{\hbar}[\hat{H},\hat{H}]=0
\end{displaymath}](img181.png) |
(26) |
e
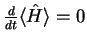 . A quantidade física associada ao hamiltoniano
é a energia. Logo, a energia se conserva, na mecânica quântica.
. A quantidade física associada ao hamiltoniano
é a energia. Logo, a energia se conserva, na mecânica quântica.
Como
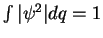 , sendo a integral estendida a todo o espaço, temos que
, sendo a integral estendida a todo o espaço, temos que
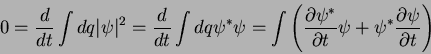 |
(27) |
Eliminando as derivadas no tempo pelo uso da equação de Schrödinger, temos:
Segue então que
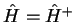 , ou seja, que
, ou seja, que 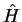 é hermiteano.
é hermiteano.



Next: O comutador de e
Up: Energia e Momento
Previous: Energia e Momento
Henrique Fleming
2003-03-30
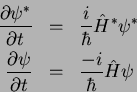
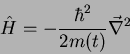
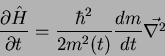
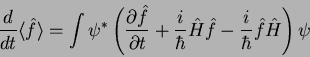
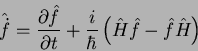
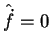 , e
, e