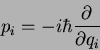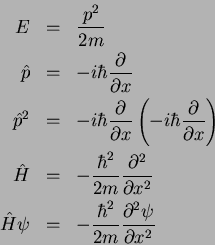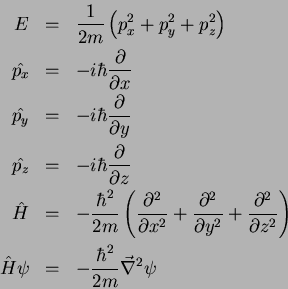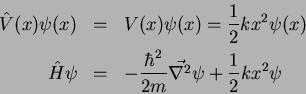Next: A derivada no tempo
Up: Mecânica Quântica
Previous: Adição e subtração de
A função de onda determina completamente o estado físico do sistema. Isto significa que,
dada a função de onda 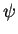 de um sistema no instante
de um sistema no instante 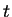 , não somente todas as propriedades
do sistema naquele instante estão descritas, mas também as propriedades em qualquer
instante subseqüente (tudo isso, naturalmente, em termos do conceito de descrição completa admitido
pela mecânica quântica). Matematicamente isto quer dizer que a derivada primeira no tempo,
, não somente todas as propriedades
do sistema naquele instante estão descritas, mas também as propriedades em qualquer
instante subseqüente (tudo isso, naturalmente, em termos do conceito de descrição completa admitido
pela mecânica quântica). Matematicamente isto quer dizer que a derivada primeira no tempo,
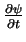 no instante
no instante 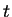 é determinada pelo valor de
é determinada pelo valor de 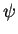 no mesmo instante.
Como a teoria é linear, essa relação é também linear. Vamos escrevê-la assim:
no mesmo instante.
Como a teoria é linear, essa relação é também linear. Vamos escrevê-la assim:
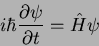 |
(13) |
onde 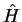 é um operador linear a ser determinado. A maneira mais direta de descobrir a natureza
de
é um operador linear a ser determinado. A maneira mais direta de descobrir a natureza
de 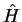 é impôr que, no limite clássico, as leis de Newton sejam obtidas. Usando argumentos de
mecânica avançada mostra-se que
é impôr que, no limite clássico, as leis de Newton sejam obtidas. Usando argumentos de
mecânica avançada mostra-se que 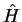 deve ser o hamiltoniano do sistema, ou seja, a energia
escrita em termos dos momentos
deve ser o hamiltoniano do sistema, ou seja, a energia
escrita em termos dos momentos 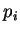 e das coordenadas
e das coordenadas 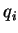 do sistema, fazendo-se ainda
a substituição
do sistema, fazendo-se ainda
a substituição
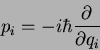 |
(14) |
Exemplos:
(1) A partícula livre unidimensional:
Equação de Schrödinger completa:
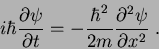 |
(15) |
(2) A partícula livre tri-dimensional:
Equação de Schrödinger completa:
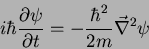 |
(16) |
(3) Partícula sobre a ação de um potencial:
Seja 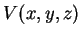 a energia potencial da partícula. Na mecânica quântica o operador
energia potencial,
a energia potencial da partícula. Na mecânica quântica o operador
energia potencial,
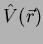 é definido por:
é definido por:
ou seja, a ação do operador
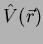 sobre a função
sobre a função 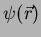 consiste
simplesmente em multiplicá-la pelo número
consiste
simplesmente em multiplicá-la pelo número 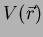 . Exemplo:
. Exemplo:
Oscilador harmônico unidimensional:
Exercício: Mostre que o hamiltoniano do oscilador harmônico é hermiteano.
Subsections



Next: A derivada no tempo
Up: Mecânica Quântica
Previous: Adição e subtração de
Henrique Fleming
2003-03-30