


Next: Algumas técnicas matemáticas
Up: Energia e Momento
Previous: A derivada no tempo
Como
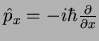 , temos
, temos
![\begin{displaymath}[\hat{x}, \hat{p}_x]\psi(x)=\hat{x}(-i\hbar) \frac{\partial \...
...}-
(-i\hbar)\frac{\partial}{\partial x}\left(x\psi(x)\right)
\end{displaymath}](img190.png) |
(28) |
que leva a
![\begin{displaymath}[\hat{x}, \hat{p}_x]\psi(x)=i\hbar \psi(x)
\end{displaymath}](img191.png) |
(29) |
Logo, temos a igualdade entre operadores:
![\begin{displaymath}[\hat{x},\hat{p}_x]=i\hbar \hat{1}
\end{displaymath}](img192.png) |
(30) |
onde 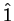 é o operador unidade, definido por
é o operador unidade, definido por
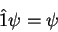 |
(31) |
qualquer que seja 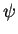 .
Obviamente isto vale também para as outras componentes.
Numa forma geral. temos:
.
Obviamente isto vale também para as outras componentes.
Numa forma geral. temos:
![\begin{displaymath}[\hat{p}_i, \hat{q}_j]=-i\hbar \delta_{ij}\hat{1}
\end{displaymath}](img195.png) |
(32) |
São as chamadas relações de Heisenberg.
Henrique Fleming
2003-03-30