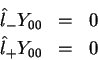Next: Potenciais com simetria central
Up: Autofunções simultâneas do momento
Previous: Autofunções simultâneas do momento
Chamaremos de operadores vetoriais operadores do tipo
e que satisfazem as seguintes relações de comutação com as componentes do
momento angular:
![\begin{displaymath}[\hat{l}_a, \hat{T}_b]= i\epsilon_{abc}\hat{T}_c
\end{displaymath}](img443.png) |
(103) |
onde a costumeira convenção indica uma soma sobre os valores do índice  ,
e, sendo
,
e, sendo 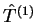 e
e 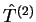 dois operadores desse tipo,
dois operadores desse tipo,
![\begin{displaymath}[\hat{l}_i, \hat{T}^{(1)}_{j}\hat{T}^{(2)}_{j}]=0
\end{displaymath}](img447.png) |
(104) |
Exemplos: 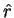 ,
,  e
e 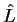 são, todos, operadores vetoriais.
Das relações acima segue, em particular, que, para qualquer operador vetorial
são, todos, operadores vetoriais.
Das relações acima segue, em particular, que, para qualquer operador vetorial  ,
,
![\begin{displaymath}[\hat{l}_i,\hat{T}_j\hat{T}_j]=0
\end{displaymath}](img451.png) |
(105) |
Seja  um operador vetorial. Será útil introduzir um ``operador escada'', da seguinte forma:
um operador vetorial. Será útil introduzir um ``operador escada'', da seguinte forma:
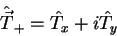 |
(106) |
Facilmente se verifica que
![\begin{displaymath}[\hat{l}_z,\hat{T}_{+}]=\hat{T}_{+}
\end{displaymath}](img454.png) |
(107) |
bem como
![\begin{displaymath}[\hat{l}_x,\hat{T}_{+}]=-\hat{T}_z
\end{displaymath}](img455.png) |
(108) |
![\begin{displaymath}[\hat{l}_y,\hat{T}_{+}]=-i\hat{T}_z
\end{displaymath}](img456.png) |
(109) |
Vamos agora calcular o comutador
![$[\hat{\vec{L}}²,\hat{T}_{+}]$](img457.png) . Lembrando que
. Lembrando que
e usando as relações acima, temos, após um pouco de paciência,
![\begin{displaymath}[\hat{\vec{l}}^2,\hat{T}_{+}]=2[\hat{T}_{+}\hat{l}_z-\hat{T}_z\hat{l}_{+}]+2\hat{T}_{+}
\end{displaymath}](img459.png) |
(110) |
Sejam 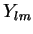 as autofunções de
as autofunções de
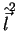 e, em
particular, seja
e, em
particular, seja 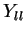 aquela com máximo valor de
aquela com máximo valor de 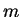 , para um
dado
, para um
dado 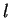 . Vamos mostrar que
. Vamos mostrar que
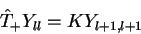 |
(111) |
onde  é uma constante.
é uma constante.
De fato,
 |
(112) |
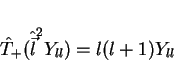 |
(113) |
Ora, o operador
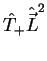 pode ser escrito
assim:
pode ser escrito
assim:
![\begin{displaymath}
\hat{T}_{+}\hat{\vec{l}}^2 =
\hat{T}_{+}\hat{\vec{l}}^2...
...}=
[\hat{T}_{+},\hat{\vec{l}}^2]+\hat{\vec{l}}^2\hat{T}_{+}
\end{displaymath}](img466.png) |
(114) |
Logo,a Eq.(113) pode ser escrita
![\begin{displaymath}[\hat{T}_{+},\hat{\vec{l}}^2]Y_{ll}+
\hat{\vec{l}}^2(\hat{T}_{+}Y_{ll})=l(l+1)Y_{ll}
\end{displaymath}](img467.png) |
(115) |
Usando a Eq.(110),
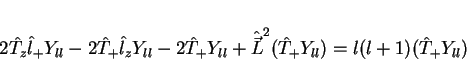 |
(116) |
Como
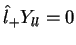 , obtemos sem dificuldade que
, obtemos sem dificuldade que
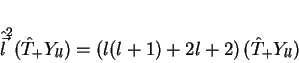 |
(117) |
ou, finalmente,
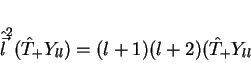 |
(118) |
que significa que
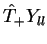 é autofunção de
é autofunção de
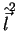 de autovalor
de autovalor 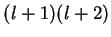 . Logo,
. Logo,
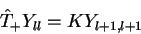 |
(119) |
Este resultado mostra que, se determinarmos 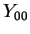 , seremos
capazes de construir
, seremos
capazes de construir 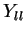 para qualquer
para qualquer 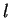 , sem ter de
resolver equações diferenciais.
Para determinar
, sem ter de
resolver equações diferenciais.
Para determinar
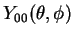 note-se que
note-se que
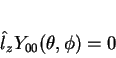 |
(120) |
e
Daí segue facilmente que
Dessas duas e da Eq.(120), segue que
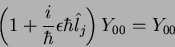 |
(123) |
para 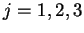 . Isto quer dizer que
. Isto quer dizer que 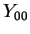 é invariante por
rotações infinitesimais em torno dos eixos
é invariante por
rotações infinitesimais em torno dos eixos 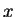 ,
, 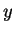 ,
, 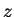 , ou seja,
é invariante por qualquer rotação infinitesimal. Logo, é
esfericamente simétrica, não podendo depender de
, ou seja,
é invariante por qualquer rotação infinitesimal. Logo, é
esfericamente simétrica, não podendo depender de 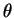 ou
ou
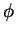 . Mas essas são as suas únicas variáveis. Portanto,
. Mas essas são as suas únicas variáveis. Portanto, 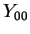 é constante. A menos de normalização, podemos então tomar
é constante. A menos de normalização, podemos então tomar
Considere o operador vetorial 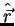 , e vamos construir o operador
, e vamos construir o operador
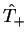 associado a ele, que seria o operador
associado a ele, que seria o operador
Como os operadores 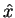 e
e 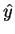 são multiplicativos,
vamos cometer um ligeiro abuso de notação, omitindo a
``casinha''(acento circunflexo, versão chinesa). Assim,
escreveremos, sem a menor cerimônia,
são multiplicativos,
vamos cometer um ligeiro abuso de notação, omitindo a
``casinha''(acento circunflexo, versão chinesa). Assim,
escreveremos, sem a menor cerimônia,
deixando claro que se trata de operadores. Já que estamos com a mão na massa,
vamos estudar, em lugar de 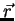 , o operador
, o operador
 . O operador
. O operador
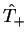 associado a ele é
associado a ele é
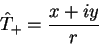 |
(124) |
Temos, então,
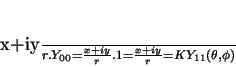 |
(125) |
ou seja,
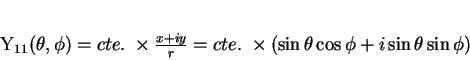 |
(126) |
ou ainda,
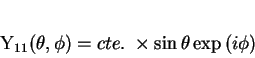 |
(127) |
De uma maneira geral, teremos:
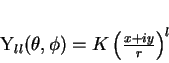 |
(128) |
Para obter 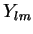 basta fazer uso do operador
basta fazer uso do operador 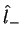 .
.
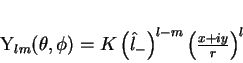 |
(129) |



Next: Potenciais com simetria central
Up: Autofunções simultâneas do momento
Previous: Autofunções simultâneas do momento
Henrique Fleming
2003-03-30
![$[\hat{\vec{L}}²,\hat{T}_{+}]$](img457.png) . Lembrando que
. Lembrando que