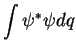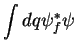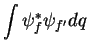Next: Operadores unitários e simetrias
Up: Mecânica Quântica
Previous: Integral de Fourier
A equação de Schrödinger de um sistema físico de hamiltoniano
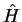 é
é
Suponhamos que 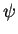 seja um estado estacionário, ou seja, que
seja um estado estacionário, ou seja, que
Inserindo-se esta expressão na equação de Schrödinger, obtém-se
uma equação para 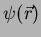 , que é
, que é
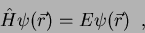 |
(43) |
conhecida como equação de Schrödinger independente do tempo.
Resolvê-la é determinar o par
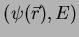 , onde
, onde 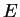 é um
número.
Para exemplificar, vamos tratar um caso muto simples: uma
partícula livre, de massa
é um
número.
Para exemplificar, vamos tratar um caso muto simples: uma
partícula livre, de massa 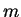 , que se move ao longo do eixo
, que se move ao longo do eixo 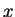 .
Neste caso
.
Neste caso
e a Eq.(43) é
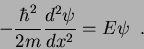 |
(44) |
Introduzindo
podemos reescrever a equação acima assim:
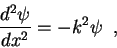 |
(45) |
cuja solução geral é
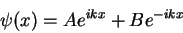 |
(46) |
com 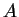 e
e 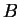 arbitrários. Existe solução para todo
arbitrários. Existe solução para todo 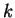 , e, como
, e, como
existe solução para todo  . Diz-se então que o espectro é
contínuo.
Seja
. Diz-se então que o espectro é
contínuo.
Seja 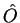 um operador associado a uma quantidade física de
espectro contínuo. Escreveremos a equação de autovalores assim:
um operador associado a uma quantidade física de
espectro contínuo. Escreveremos a equação de autovalores assim:
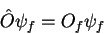 |
(47) |
onde o índice 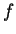 agora varia continuamente. Como veremos mais
tarde, as autofunções associadas a um espectro contínuo não são
normalizáveis, isto é, não é possível impor para elas a condição
agora varia continuamente. Como veremos mais
tarde, as autofunções associadas a um espectro contínuo não são
normalizáveis, isto é, não é possível impor para elas a condição
Exemplo: a função de onda de um estado estacionário de
uma partícula livre, cuja parte espacial vimos na
Eq.(46), é
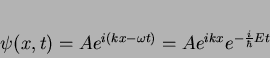 |
(48) |
onde usamos
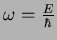 . Então
. Então
e, por isso,
A seguir vamos descobrir uma maneira de normalizar adequadamente
as autofunções ligadas a um espectro contínuo.
Seja 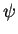 uma função de onda normalizável. A
expansão dela em autofunções da quantidade física
uma função de onda normalizável. A
expansão dela em autofunções da quantidade física 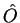 , cujo
espectro é contínuo, é
, cujo
espectro é contínuo, é
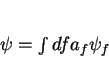 |
(49) |
Queremos que  seja a probabilidade de que, efetuada uma
medida de
seja a probabilidade de que, efetuada uma
medida de 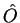 , o valor obtido esteja entre
, o valor obtido esteja entre 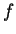 e
e 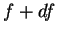 .
Logo,
.
Logo,
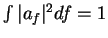 . Da mesma forma,
. Da mesma forma,
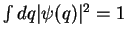 . Segue que
. Segue que
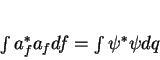 |
(50) |
e, como
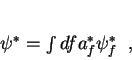 |
(51) |
também que
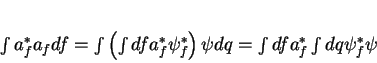 |
(52) |
Comparando o primeiro termo com o último, temos
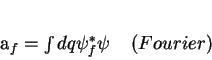 |
(53) |
que permite calcular os coeficientes da expansão
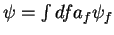 .
Rescrevendo a expansão acima como
.
Rescrevendo a expansão acima como
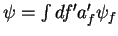 e usando-a na Eq.(53),
temos
e usando-a na Eq.(53),
temos
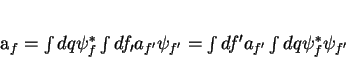 |
(54) |
Mas
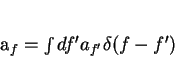 |
(55) |
Comparando as duas últimas, obtém-se
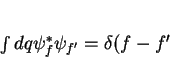 |
(56) |
que é a relação de ortogonalidade para autofunções do espectro
contínuo. Conseqüentemente, as relações básicas para o espectro
contínuo são:



Next: Operadores unitários e simetrias
Up: Mecânica Quântica
Previous: Integral de Fourier
Henrique Fleming
2003-03-30