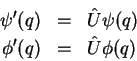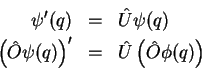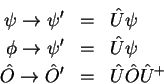Next: Exemplos de operadores unitários
Up: Mecânica Quântica
Previous: O espectro contínuo
As quantidades observáveis (resultados de medidas) aparecem, na
mecânica quântica, sob a forma de produtos escalares de estados,
Um caso particular importante é um ``elemento de matriz'' de um
operador 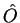 :
:
Como toda teoria, a mecânica quântica admite transformações ``de
linguagem'': por exemplo, quando eu descrevo o mesmo fenômeno
usando dois sistemas de eixos ortogonais, obtenho descrições
distintas do mesmo fenômeno. Essas descrições devem ser
equivalentes, já que representam a mesma coisa de pontos-de-vista
distintos. É como se eu descrevesse o mesmo fenômeno em inglês e
em alemão: as descrições são diferentes, mas têm o mesmo conteúdo.
Como as quantidades físicas são representadas pelos produtos
escalares de estados, é importante o estudo dos operadores que
conservam os produtos escalares, ou seja, dos operadores 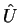 que são tais que
que são tais que
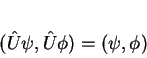 |
(61) |
ou, mais explicitamente,
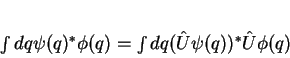 |
(62) |
Um operador linear é unitário, por definição, se
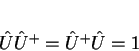 |
(63) |
Seja 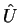 um operador unitário e considere as transformações
de funções de onda:
um operador unitário e considere as transformações
de funções de onda:
Então,
o que mostra que uma transformação implementada por um operador
unitário conserva os produtos escalares. Mais detalhadamente,
considere o produto escalar
Sejam
Podemos escrever
Logo,
Podemos interpretar este resultado assim: considere as
transformações
Então, temos:
onde
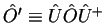 é a
transformação de
é a
transformação de 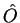 pela ação do operador linear
pela ação do operador linear 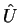 .
Diz-se que um operador
.
Diz-se que um operador 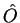 é invariante por uma
transformação unitária
é invariante por uma
transformação unitária 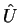 se
se
ou, equivalentemente, se
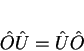 |
(64) |
Subsections



Next: Exemplos de operadores unitários
Up: Mecânica Quântica
Previous: O espectro contínuo
Henrique Fleming
2003-03-30