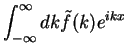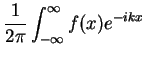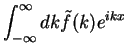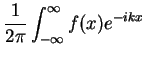Next: O espectro contínuo
Up: Algumas técnicas matemáticas
Previous: A função delta de
A integral de Fourier é
instrumento fundamental na mecânica quântica. Trata-se de uma
extensão das séries de Fourier que permite obter expansões de
funções que não são periódicas. Este não é o lugar para se
adquirir fluência no uso, e uma boa compreensão dos métodos da
análise de Fourier. O leitor deverá dedicar algum estudo a este
tópico, presente em todos os livros de física-matemática. De minha
parte recomendo o livro de Arnold Sommerfeld, Partial
Differential Equations of Physics. Um belíssimo livro de
matemática sobre este mesmo tema, é Körner, Fourier
Analysis, um dos livros mais bonitos que já li.
A integral, ou transformada, de Fourier de uma função 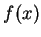 , é
uma função
, é
uma função 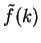 a ela ligada pelas relações
a ela ligada pelas relações
Pode-se verificar a consistência dessas relações com o uso da
funçao 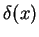 :
:
A transformada de Fourier de uma função constante, 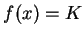 , é:
, é:
ou seja, a transformada de Fourier de uma constante é um múltiplo
de 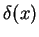 . Um outro resultado importante é a transformada de
Fourier de uma gaussiana: seja
. Um outro resultado importante é a transformada de
Fourier de uma gaussiana: seja
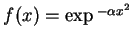 . Sua
transformada de Fourier é
. Sua
transformada de Fourier é
ou seja, a transformada de Fourier de uma gaussiana é outra
gaussiana.



Next: O espectro contínuo
Up: Algumas técnicas matemáticas
Previous: A função delta de
Henrique Fleming
2003-03-30