Next: Exemplos
Up: oticag
Previous: Equações de Maxwell
Vamos procurar soluções da forma
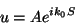 |
(6) |
com
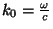 , onde
, onde 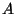 e
e 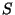 são funções de
são funções de 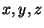 que
variam lentamente e que não tendem a
que
variam lentamente e que não tendem a 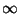 quando
quando 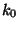 cresce.
cresce.
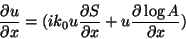 |
(7) |
com termos análogos para as derivadas em 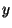 e
e 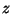 . Assim, temos
. Assim, temos
Isto pode ser abreviado assim:
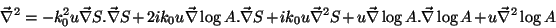 |
(10) |
Logo, a equação fica:
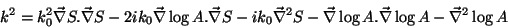 |
(11) |
ou ainda,
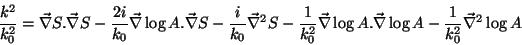 |
(12) |
No limite
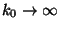 , temos
, temos
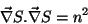 |
(13) |
e
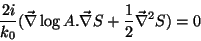 |
(14) |
de maneira que as equações são:
que são as equações básicas da ótica geométrica.1



Next: Exemplos
Up: oticag
Previous: Equações de Maxwell
Henrique Fleming
2002-04-24
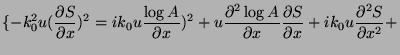
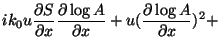
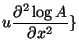
![$\displaystyle \{-k_0^2u[(\frac{ \partial S}{\partial x})^2
+ (\frac{ \partial S}{\partial y})^2 +(\frac{ \partial S}{\partial z})^2
] +$](img34.png)
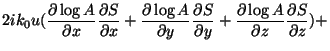
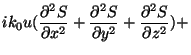
![$\displaystyle u[(\frac{ \partial\log{A}}{\partial x})^2 +
(\frac{ \partial\log{A}}{\partial y})^2+
(\frac{ \partial\log{A}}{\partial z})^2] +$](img37.png)