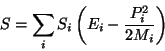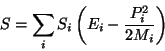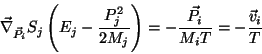Next: Outro exemplo : correntes
Up: Máximos e mínimos para
Previous: Exemplo simples
Como primeira aplicação, vamos determinar que movimentos um corpo
(sistema macroscópico) pode executar no equilíbrio termodinâmico,
ou seja, sob a condição de que a entropia seja um máximo. Seguimos o
tratamento do problema dado por Landau [5]. Dividimos o corpo
em um grande número de partes pequenas (mas ainda macroscópicas),
e sejam 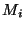 ,
, 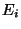 e
e 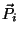 a massa, a energia e o momento da
a massa, a energia e o momento da
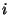 -ésima parte. A entropia de cada parte é uma função de sua
energia interna, isto é, da diferença entre sua energia total
-ésima parte. A entropia de cada parte é uma função de sua
energia interna, isto é, da diferença entre sua energia total 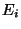 e sua energia cinética, dada por
e sua energia cinética, dada por
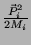 . A
entropia total do corpo, portanto, pode ser escrita
. A
entropia total do corpo, portanto, pode ser escrita
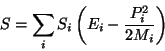 |
(20) |
Supondo que o corpo seja um sistema isolado, o momento e o momento
angular devem ser conservados. Temos, portanto, dois vínculos:
onde 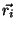 é o vetor de posição da
é o vetor de posição da 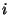 -ésima parte do corpo.
As condições de vínculo são duas condições vetoriais, portanto, na
realidade, seis condições escalares. Logo, são necessários seis
multiplicadores de Lagrange. Mas podemos reuní-los em dois vetores,
denotados por
-ésima parte do corpo.
As condições de vínculo são duas condições vetoriais, portanto, na
realidade, seis condições escalares. Logo, são necessários seis
multiplicadores de Lagrange. Mas podemos reuní-los em dois vetores,
denotados por 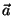 e
e 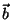 . Para determinar o máximo da
entropia na presença desses dois vínculos vetoriais, devemos,
então, igualar a zero as derivadas parciais da função
. Para determinar o máximo da
entropia na presença desses dois vínculos vetoriais, devemos,
então, igualar a zero as derivadas parciais da função
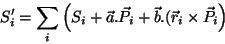 |
(23) |
onde 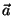 e
e 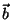 são dois vetores constantes a determinar.
A entropia deve ser um máximo em função das energias internas. Derivar
em relação à energia interna é equivalente a derivar em relação aos
momentos, logo, para o nosso problema,
as variáveis são as componentes
são dois vetores constantes a determinar.
A entropia deve ser um máximo em função das energias internas. Derivar
em relação à energia interna é equivalente a derivar em relação aos
momentos, logo, para o nosso problema,
as variáveis são as componentes 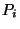 do momento. Por isso
devemos ter
do momento. Por isso
devemos ter
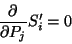 |
(24) |
ou, mais sucintamente,
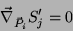 |
(25) |
onde
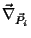 é o gradiente na variável
é o gradiente na variável
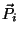 ,
ou seja, o operador vetorial
,
ou seja, o operador vetorial
denotando por
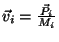 a velocidade da
a velocidade da
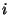 -ésima parte do corpo, temos (veja o cálculo detalhado
no apêndice)
-ésima parte do corpo, temos (veja o cálculo detalhado
no apêndice)
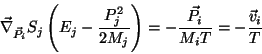 |
(26) |
onde 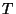 é a temperatura absoluta, e usamos o fato de que
é a temperatura absoluta, e usamos o fato de que
considerando-se a entropia como função da energia interna e do volume.
O cálculo das derivadas parciais da função 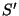 , na
Eq.(23), pode agora ser feito sem maiores dificuldades.
Obtém-se
, na
Eq.(23), pode agora ser feito sem maiores dificuldades.
Obtém-se
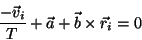 |
(27) |
onde usamos
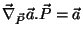 e que
e que
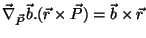 .
Introduzindo as notações
.
Introduzindo as notações
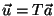 e
e
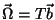 ,
temos então:
,
temos então:
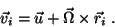 |
(28) |
O significado físico é claro: o movimento das partes do corpo que
é compatível com o equilíbrio é composto de uma translação do
corpo
como um todo, e de uma rotação, como um todo, com velocidade angular
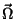 .
.
Por que, então, as massas fluidas em torno de nós não estão
se movimentando apenas dessa maneira? Por que não são um sistema
isolado: tanto o bombeamento de energia do Sol quanto a ação da
gravidade da Terra são ações externas, e, nessas condições, a entropia
não tem a obrigação de estar num máximo. Enquanto é fácil
blindar o sistema contra a luz do Sol, isto é muito mais difícil no
caso do campo gravitacional. A ação combinada do Sol e da gravidade da
Terra produz toda a sorte de movimentos ``proibidos'', como as correntes
de convecção nos mares e ares (estas últimas popularmente conhecidas
como vento...). Uma aplicação interessante do resultado que obtivemos
é o crescimento de cristais em estações espaciais. Como elas estão em
queda livre, o campo gravitacional é eliminado; sendo o ambiente
fechado, a radiação solar também não está presente. Assim, se
está, nessas estações, nas condições de validade do nosso ``teorema'':
como só há rotações e translações, que são fáceis de evitar,
consegue-se crescer cristais em condições de total ausência de
convecção, o que permite obter cristais perfeitos (e enormes).
Subsections



Next: Outro exemplo : correntes
Up: Máximos e mínimos para
Previous: Exemplo simples
Henrique Fleming
2003-09-24