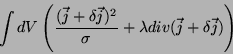Next: Bibliography
Up: Aplicações à física
Previous: Aplicações à física
Seja dado um condutor ôhmico, ou seja, tal que a relação entre
a corrente e o campo elétrico seja
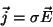 |
(29) |
onde 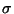 é a condutividade do material. Sabemos que a potência
dissipada no sistema é dada por
é a condutividade do material. Sabemos que a potência
dissipada no sistema é dada por
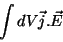 |
(30) |
Há um teorema, atribuído a Lord Kelvin, que diz que a distribuição
de correntes estacionárias em um condutor é aquela que minimiza a
potência dissipada. Vamos obter este resultado com os métodos que
desenvolvemos até aqui.
Uma distribuição de correntes se diz estacionária se
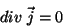 |
(31) |
Para determinar completamente 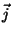 é suficiente, então, dar o
valor de
é suficiente, então, dar o
valor de 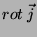 .
A potência dissipada é dada pela expressão
.
A potência dissipada é dada pela expressão
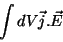 |
(32) |
O vínculo, neste caso, é a condição de estacionaridade, que é
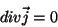 |
(33) |
O que nós queremos saber é qual função 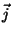 minimiza a
potência. Trata-se, portanto, de uma generalização do que fizemos até
aqui (que era, dada uma função, saber em que ponto era máxima). O problema
se resolve assim: a corrente que gera um mínimo de potência é aquela
particular corrente
minimiza a
potência. Trata-se, portanto, de uma generalização do que fizemos até
aqui (que era, dada uma função, saber em que ponto era máxima). O problema
se resolve assim: a corrente que gera um mínimo de potência é aquela
particular corrente 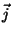 tal que, acrescentando-se uma pequena
correção
tal que, acrescentando-se uma pequena
correção 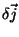 a ela, a potência não muda de valor em
primeira ordem. Trata-se de uma generalização imediata do caso anterior. De fato,
o ponto em que uma função tem um mínimo (ou máximo) goza da seguinte propriedade:
mudando-se ligeiramente essa posição, o valor da função não se altera em
primeira ordem (é este o significado de a derivada se anular).Então,
exigir que a ``variação'' da função seja zero em primeira ordem, é
equivalente a exigir que as derivadas primeiras se anulem.
Seja
a ela, a potência não muda de valor em
primeira ordem. Trata-se de uma generalização imediata do caso anterior. De fato,
o ponto em que uma função tem um mínimo (ou máximo) goza da seguinte propriedade:
mudando-se ligeiramente essa posição, o valor da função não se altera em
primeira ordem (é este o significado de a derivada se anular).Então,
exigir que a ``variação'' da função seja zero em primeira ordem, é
equivalente a exigir que as derivadas primeiras se anulem.
Seja 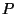 a potência dissipada. Temos
a potência dissipada. Temos
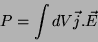 |
(34) |
Substituímos agora 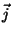 por
por
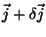 , onde
, onde
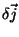 é um infinitésimo. Obtemos uma nova potência
é um infinitésimo. Obtemos uma nova potência
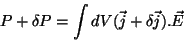 |
(35) |
A variação de 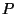 é
é
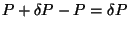 , com
, com
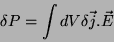 |
(36) |
Para a corrente que minimiza a potência, devemos ter
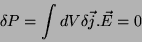 |
(37) |
É claro que a corrente que minimiza a potência é a corrente zero.
Mas o que nós queremos é saber qual a corrente não-nula e
estacionária que minimiza a potência. Temos então que impor o
vínculo
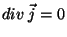 . A expressão cuja variação em primeira
ordem deve ser zero é
. A expressão cuja variação em primeira
ordem deve ser zero é
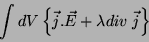 |
(38) |
onde 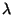 é um multiplicador de Lagrange. Porém, neste caso,
o multiplicador de Lagrange deve ser uma função
é um multiplicador de Lagrange. Porém, neste caso,
o multiplicador de Lagrange deve ser uma função
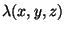 em vez de
um número, como no caso anterior. Acrescentando-se um
em vez de
um número, como no caso anterior. Acrescentando-se um 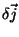 à corrente e usando
à corrente e usando
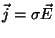 , temos :
, temos :
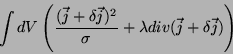 |
(39) |
cuja variação em primeira ordem, que devemos igualar a zero, é:
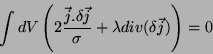 |
(40) |
Resta colocar o último termo da integral numa forma mais reveladora.
Temos
Logo, a integral (40) pode ser escrita
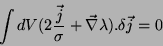 |
(41) |
onde a parte do integrando que contém um divergente foi desprezada
por razões bem conhecidas (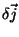 se anula no infinito).
Como
se anula no infinito).
Como 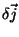 é arbitrário, devemos ter
é arbitrário, devemos ter
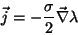 |
(42) |
ou
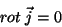 |
(43) |
que completa a determinação da corrente. Como estas são as equaçõeses
para correntes estacionárias ôhmicas usuais, o teorema está
provado: as correntes ôhmicas estacionárias que minimizam a potência
dissipada são aquelas para as quais
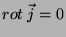 (em última análise,
são aquelas para as quais
(em última análise,
são aquelas para as quais 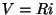 ).
).



Next: Bibliography
Up: Aplicações à física
Previous: Aplicações à física
Henrique Fleming
2003-09-24