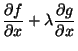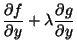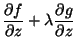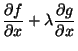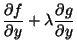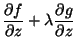Next: Aplicações à física
Up: O método
Previous: Multiplicadores de Lagrange
Voltemos ao problema do paralelepípedo e vamos resolvê-lo pelo
método de Lagrange.
A função cujos máximos procuramos é 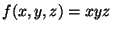 ; o vínculo
é
; o vínculo
é
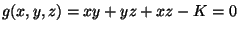 . Logo, temos de igualar a zero as derivadas
parciais da função
. Logo, temos de igualar a zero as derivadas
parciais da função 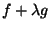 . Um cálculo simples leva a
. Um cálculo simples leva a
Das duas primeiras temos
de onde segue imediatamente que 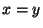 . Das duas últimas, analogamente,
segue que
. Das duas últimas, analogamente,
segue que 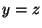 . Logo,
. Logo, 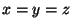 , e se trata de um cubo. Note-se que não
foi
sequer necessário calcular
, e se trata de um cubo. Note-se que não
foi
sequer necessário calcular 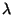 . Assim, mesmo neste caso muito
simples, é vantajoso usar o método dos multiplicadores de Lagrange.
. Assim, mesmo neste caso muito
simples, é vantajoso usar o método dos multiplicadores de Lagrange.
Henrique Fleming
2003-09-24