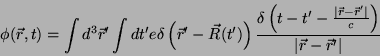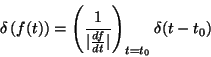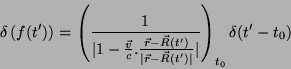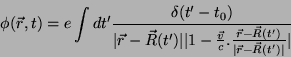Next: O dipolo de Hertz
Up: RADIAÇÃO
Previous: A função de Green
Queremos calcular agora o potencial de uma carga puntiforme
de valor 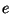 cuja posição, variável com o tempo, é descrita
pelo vetor
cuja posição, variável com o tempo, é descrita
pelo vetor 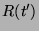 . Logo,
. Logo,
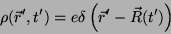 |
(5) |
e a expressão para 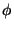 fica
fica
 |
(6) |
A integração em  é imediata, dando
é imediata, dando
 |
(7) |
Resta calcular a integral em  , o que passamos a fazer.
O integrando possui uma
, o que passamos a fazer.
O integrando possui uma
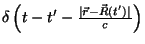 que é da forma geral
que é da forma geral
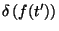 , com
, com
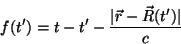 |
(8) |
Seja 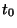 o valor de
o valor de 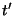 tal que
tal que
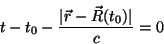 |
(9) |
A fórmula a ser usada é
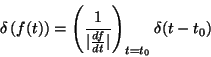 |
(10) |
Realizamos este cálculo no Apêndice. O resultado é:
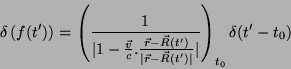 |
(11) |
onde introduzimos a notação
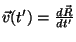 .
Levando este resultado à Eq.(7), temos
.
Levando este resultado à Eq.(7), temos
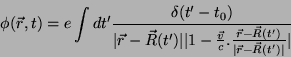 |
(12) |
ou,
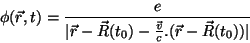 |
(13) |
Um cálculo análogo dá
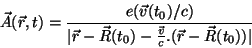 |
(14) |
As Eqs.(13) e (14) são os potenciais de Liénard-
Wiechert: são os potenciais eletromagnéticos de uma carga puntiforme
com movimento arbitrário, sua posição sendo descrita pela função vetorial
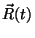 . São resultados muito importantes, por sua generalidade. Vamos
fazer uso deles para estudar, a seguir, o dipolo oscilante de Hertz. O cálculo dos
campos
. São resultados muito importantes, por sua generalidade. Vamos
fazer uso deles para estudar, a seguir, o dipolo oscilante de Hertz. O cálculo dos
campos 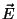 e
e 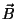 correspondentes às Eqs.(13) e (14)
é um tanto complicado. Por isso, será feito no Apêndice. O leitor interessado
fará bem em estudar também essa parte, pois contém a demonstração de um
fato muito importante: uma carga acelerada irradia.
correspondentes às Eqs.(13) e (14)
é um tanto complicado. Por isso, será feito no Apêndice. O leitor interessado
fará bem em estudar também essa parte, pois contém a demonstração de um
fato muito importante: uma carga acelerada irradia.



Next: O dipolo de Hertz
Up: RADIAÇÃO
Previous: A função de Green
Henrique Fleming
2002-04-20