


Next: Relações de dispersão
Up: dispersion
Previous: A energia do campo
Decorrem da representação integral de
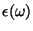 ,
Eq.(
,
Eq.(![[*]](/usr/share/latex2html/icons/crossref.png) ), que repetimos para a conveniência do leitor,
), que repetimos para a conveniência do leitor,
lembrando que 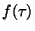 é finita pata todo
é finita pata todo 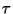 , incluíndo
, incluíndo 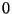 . Para dielétricos,
. Para dielétricos, 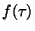 tende a zero para
tende a zero para
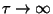 . Escrevendo
. Escrevendo
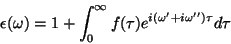 |
(21) |
vê-se que
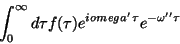 |
(22) |
indica que
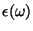 é analítica em
é analítica em 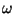 para
para
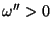 ; para
; para 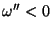 a representação integral não é válida,
e os valores de
a representação integral não é válida,
e os valores de 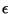 no semiplano inferior
no semiplano inferior 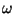 devem ser obtidos
por prolongamento analítico do semiplano superior. Haverá, em geral,
singularidades. No eixo real (
devem ser obtidos
por prolongamento analítico do semiplano superior. Haverá, em geral,
singularidades. No eixo real (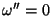 ),
),
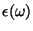 não tem
singularidades, pois, para
não tem
singularidades, pois, para 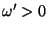 , temos valores físicos de
, temos valores físicos de
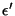 , que é função par de
, que é função par de 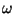 . Na origem não há
singularidades para dielétricos, mas há um polo para condutores (ver abaixo).
. Na origem não há
singularidades para dielétricos, mas há um polo para condutores (ver abaixo).
Note-se que a analiticidade de 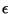 no semiplano superior é uma
conseqüência do fato de a integração em
no semiplano superior é uma
conseqüência do fato de a integração em 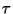 ser de
ser de 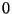 a
a 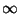 , e
não de
, e
não de  a
a 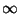 . Logo, essa analiticidade é uma
conseqüência da em causalidade.
. Logo, essa analiticidade é uma
conseqüência da em causalidade.
Os teoremas básicos usados nessa análise são os seguintes:
1.Titchmarsh, 2.83[1]
Let 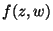 be a continuous function of the complex variables
be a continuous function of the complex variables 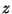 and
and
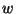 , where
, where 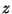 ranges over a region
ranges over a region 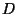 , and
, and 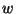 lies on a contour
lies on a contour 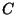 .
Let
.
Let 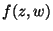 be an analytic function of
be an analytic function of  in
in 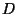 , for every value of
, for every value of 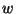 on
on 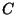 . Then
. Then
is an analytic function of  in
in 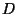 , and
, and
and similarly for higher derivatives.
No nosso caso
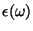 é definido pela Eq.(
é definido pela Eq.(![[*]](/usr/share/latex2html/icons/crossref.png) ), que
envolve uma integral num contorno (semi-eixo real positivo). As variáveis
), que
envolve uma integral num contorno (semi-eixo real positivo). As variáveis
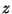 e
e 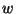 do teorema são, respectivamente,
do teorema são, respectivamente, 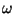 e
e 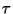 . Para mostrar
que
. Para mostrar
que
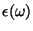 é analítica para
é analítica para
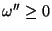 , temos de
mostrar que:
, temos de
mostrar que:
1.
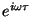 é analítica em
é analítica em 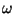 para
para 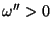 e para todo
e para todo
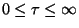 . Óbvio.
. Óbvio.
2.
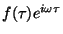 é uma função contínua de
é uma função contínua de 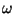 e
e 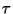 para
para 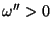 e
e
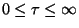 .
.
Contudo, há o problema da convergência da integral. Por isso, temos de usar
um outro teorema (Titchmarsh 2.84)[1]:
Let 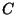 be a contour going to
be a contour going to 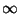 . Suppose that the
conditions of the precedent theorem are satisfied on any bounded part of
. Suppose that the
conditions of the precedent theorem are satisfied on any bounded part of
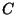 , and that
, and that
is uniformly convergent. Then the results of the previous theorem still hold.
Ora,
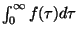 é convergente por hipótese.
é convergente por hipótese.
 é mais
convergente ainda, para
é mais
convergente ainda, para 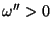 , do que a anterior. Logo, é
uniformemente convergente.(É majorada por uma integral uniformemente
convergente).
, do que a anterior. Logo, é
uniformemente convergente.(É majorada por uma integral uniformemente
convergente).



Next: Relações de dispersão
Up: dispersion
Previous: A energia do campo
Henrique Fleming
2003-03-21
![]() no semiplano superior é uma
conseqüência do fato de a integração em
no semiplano superior é uma
conseqüência do fato de a integração em ![]() ser de
ser de ![]() a
a ![]() , e
não de
, e
não de ![]() a
a ![]() . Logo, essa analiticidade é uma
conseqüência da em causalidade.
. Logo, essa analiticidade é uma
conseqüência da em causalidade.
![]() be a continuous function of the complex variables
be a continuous function of the complex variables ![]() and
and
![]() , where
, where ![]() ranges over a region
ranges over a region ![]() , and
, and ![]() lies on a contour
lies on a contour ![]() .
Let
.
Let ![]() be an analytic function of
be an analytic function of ![]() in
in ![]() , for every value of
, for every value of ![]() on
on ![]() . Then
. Then