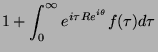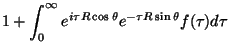Next: Meios transparentes
Up: dispersion
Previous: Propriedades analíticas de
Considere a integral
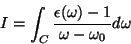 |
(23) |
no pano complexo 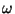 . O ponto
. O ponto 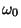 é um valor real
e positivo de
é um valor real
e positivo de 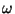 . O contorno percorre o eixo real de
. O contorno percorre o eixo real de
 a
a 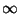 , ''salta'' o ponto
, ''salta'' o ponto 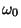 como indicado
na figura, e se fecha
por um semi-círculo de raio
como indicado
na figura, e se fecha
por um semi-círculo de raio 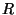 no semiplano superior. Toma-se
depois o limite
no semiplano superior. Toma-se
depois o limite
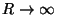 .
.
Pela analiticidade de
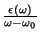 no
interior do contorno, temos
no
interior do contorno, temos 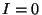 . A integral no círculo grande é
zero, pois tomando
. A integral no círculo grande é
zero, pois tomando
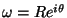 ,
,
Por outro lado,
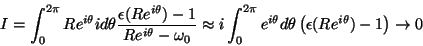 |
(28) |
Em conseqüência,
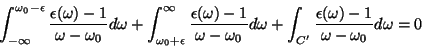 |
(29) |
onde 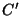 é um semiccxirculo em torno do ponto
é um semiccxirculo em torno do ponto 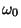 .
.
A terceira integral dá, trivialmente,
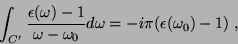 |
(30) |
no limite
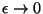 (
(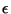 é o raio do pequeno
semiccxirculo
é o raio do pequeno
semiccxirculo  . Logo,
. Logo,
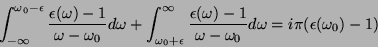 |
(31) |
e
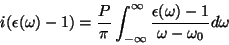 |
(32) |
onde 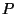 indica o valor principal de Cauchy. Tomando agora separadamente
a igualdade entre as partes reais e imaginárias, temos:
indica o valor principal de Cauchy. Tomando agora separadamente
a igualdade entre as partes reais e imaginárias, temos:
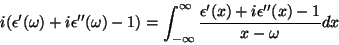 |
(33) |
de onde sai imediatamente que
que são as relacxo de Kramers [2], Kronig[3].
Estas relacxo têm inúmeras aplicacxo. Damos alguns exemplos.
1. Se um meio dielétrico não absorve em nenhuma freqencia,
também não polariza em nenhuma freqencia, ou seja, é o vácuo.
Logo, só o vácuo é totalmente transparente.
2. Se um meio se polariza, necessariamente absorve (logicamente
equivalente à anterior!).
Subsections



Next: Meios transparentes
Up: dispersion
Previous: Propriedades analíticas de
Henrique Fleming
2003-03-21