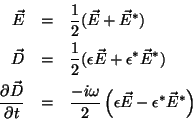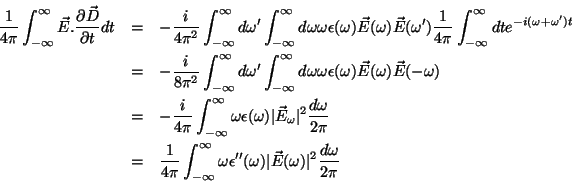Next: Propriedades analíticas de
Up: dispersion
Previous: Limite de altas freqüências
Em um meio dielétrico isotrópico de dispersão desprezível
se tem
onde 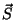 é o vetor de Poynting e
é o vetor de Poynting e 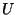 a densidade de energia,
dada por
a densidade de energia,
dada por
O resultado exato, que não depende de hipóteses sobre a
existência ou não de dispersão é:
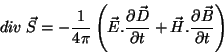 |
(11) |
Na figura acima, o retângulo tracejado delimita um trecho do meio material
onde a onda se propaga. É suposto que esse trecho é longo o
suficiente para que toda a energia da onda seja absorvida, de maneira que,
da energia que penetra no volume pela face 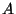 , nenhuma emerge pela face
, nenhuma emerge pela face
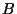 (
(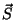 é
é 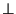 ás faces
ás faces 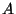 e
e 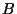 ). A integral volumétrica
de
). A integral volumétrica
de 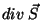 dá, então, a quantidade de energia absorvida. Como ela
é transformada em calor, há uma variação da entropia, que é, pela
segunda lei da termodinâmica, necessariamente positiva, dada por
dá, então, a quantidade de energia absorvida. Como ela
é transformada em calor, há uma variação da entropia, que é, pela
segunda lei da termodinâmica, necessariamente positiva, dada por
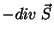 .
.
Pondo
e analogamente para 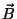 e
e 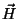 , temos
, temos
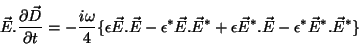 |
(12) |
Os termos em
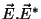 não oscilam. Os outros termos têm um
fator oscilante
não oscilam. Os outros termos têm um
fator oscilante
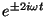 , e desaparecem na média por
período, de maneira que a contribuição finita é
, e desaparecem na média por
período, de maneira que a contribuição finita é
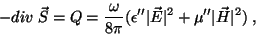 |
(13) |
representando a quantidade de calor produzida por unidade de tempo e unidade de
volume. 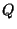 tem de ser positivo, e daí seguem os importantes resultados
tem de ser positivo, e daí seguem os importantes resultados
Mais geralmente, para o caso não-monocromático, procede-se assim:
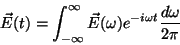 |
(16) |
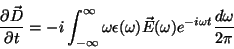 |
(17) |
com
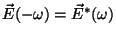 .
Vamos construir agora os os vários termos que aparecem na
Eq.(
.
Vamos construir agora os os vários termos que aparecem na
Eq.(![[*]](/usr/share/latex2html/icons/crossref.png) ).
).
onde usamos
uma vez que o integrando é função ímpar de 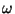 . Logo,
. Logo,
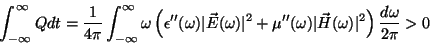 |
(18) |
com
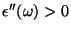 e
e
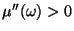 para todo
para todo 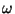 .
.



Next: Propriedades analíticas de
Up: dispersion
Previous: Limite de altas freqüências
Henrique Fleming
2003-03-21
![]() , nenhuma emerge pela face
, nenhuma emerge pela face
![]() (
(![]() é
é ![]() ás faces
ás faces ![]() e
e ![]() ). A integral volumétrica
de
). A integral volumétrica
de ![]() dá, então, a quantidade de energia absorvida. Como ela
é transformada em calor, há uma variação da entropia, que é, pela
segunda lei da termodinâmica, necessariamente positiva, dada por
dá, então, a quantidade de energia absorvida. Como ela
é transformada em calor, há uma variação da entropia, que é, pela
segunda lei da termodinâmica, necessariamente positiva, dada por
![]() .
.